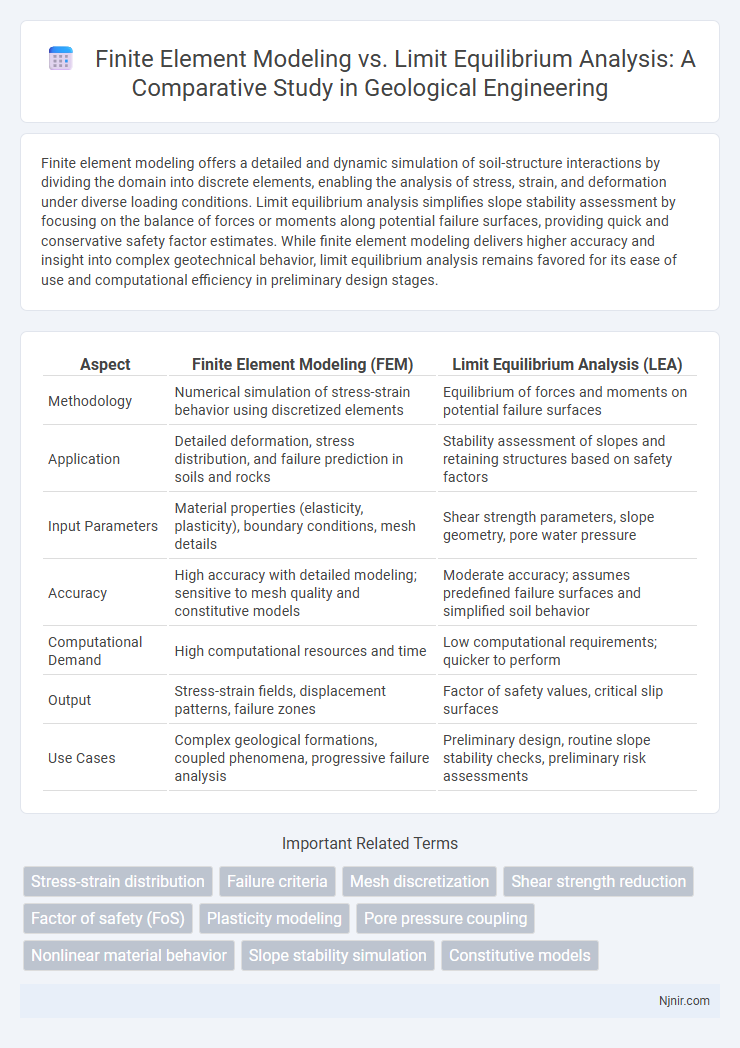
Finite element modeling offers a detailed and dynamic simulation of soil-structure interactions by dividing the domain into discrete elements, enabling the analysis of stress, strain, and deformation under diverse loading conditions. Limit equilibrium analysis simplifies slope stability assessment by focusing on the balance of forces or moments along potential failure surfaces, providing quick and conservative safety factor estimates. While finite element modeling delivers higher accuracy and insight into complex geotechnical behavior, limit equilibrium analysis remains favored for its ease of use and computational efficiency in preliminary design stages.
Table of Comparison
| Aspect | Finite Element Modeling (FEM) | Limit Equilibrium Analysis (LEA) |
|---|---|---|
| Methodology | Numerical simulation of stress-strain behavior using discretized elements | Equilibrium of forces and moments on potential failure surfaces |
| Application | Detailed deformation, stress distribution, and failure prediction in soils and rocks | Stability assessment of slopes and retaining structures based on safety factors |
| Input Parameters | Material properties (elasticity, plasticity), boundary conditions, mesh details | Shear strength parameters, slope geometry, pore water pressure |
| Accuracy | High accuracy with detailed modeling; sensitive to mesh quality and constitutive models | Moderate accuracy; assumes predefined failure surfaces and simplified soil behavior |
| Computational Demand | High computational resources and time | Low computational requirements; quicker to perform |
| Output | Stress-strain fields, displacement patterns, failure zones | Factor of safety values, critical slip surfaces |
| Use Cases | Complex geological formations, coupled phenomena, progressive failure analysis | Preliminary design, routine slope stability checks, preliminary risk assessments |
Introduction to Slope Stability Assessment Techniques
Slope stability assessment techniques encompass finite element modeling and limit equilibrium analysis, both essential for evaluating soil and rock mass behavior under stress. Finite element modeling provides a detailed stress-strain analysis through numerical simulation, capturing complex geotechnical interactions and deformation patterns. Limit equilibrium analysis simplifies stability evaluation by dividing the slope into slices, calculating safety factors based on force and moment equilibrium, commonly used for quick, practical assessments in engineering projects.
Fundamentals of Finite Element Modeling in Geological Engineering
Finite Element Modeling (FEM) in geological engineering involves discretizing soil and rock masses into finite elements to simulate stress-strain behavior under various load conditions, providing detailed insights into deformation and failure mechanisms. Unlike Limit Equilibrium Analysis (LEA), which primarily evaluates slope stability based on force and moment equilibrium, FEM accounts for complex material heterogeneity and nonlinear soil properties through constitutive models. The fundamental advantage of FEM lies in its ability to model stress distribution and displacement fields within geological structures, enabling engineers to predict localized failure zones with higher accuracy.
Overview of Limit Equilibrium Analysis Methods
Limit equilibrium analysis methods evaluate soil stability by dividing a slope into slices and assessing force and moment equilibrium to estimate the factor of safety. Common approaches include the Bishop, Janbu, and Morgenstern-Price methods, each differing in assumptions about interslice forces and equilibrium conditions. These methods are computationally efficient and widely used for routine geotechnical design, despite simplifying soil behavior compared to finite element modeling.
Key Differences Between Finite Element Modeling and Limit Equilibrium Analysis
Finite element modeling (FEM) utilizes numerical methods to simulate stress, deformation, and strain in materials by discretizing the structure into elements, providing detailed insight into internal behaviors. In contrast, limit equilibrium analysis (LEA) focuses on the balance of forces and moments to determine stability without capturing material deformation or stress distribution. FEM offers a more comprehensive, physics-based approach suited for complex geometries and material behaviors, while LEA remains efficient for preliminary slope stability assessments with simplified assumptions.
Accuracy and Reliability in Slope Stability Predictions
Finite element modeling (FEM) provides higher accuracy and reliability in slope stability predictions by simulating complex soil behaviors and stress-strain relationships under varying conditions. Limit equilibrium analysis (LEA) offers simplified, less computationally intensive solutions but may lack precision in heterogeneous or nonlinear scenarios due to its assumptions of rigid body behavior. Advanced FEM captures progressive failure mechanisms and pore-water pressure effects, making it a preferred method for detailed geotechnical assessments.
Computational Requirements and Efficiency Comparison
Finite element modeling (FEM) demands significantly higher computational resources due to its detailed stress-strain analysis and mesh refinement, resulting in longer processing times and greater memory consumption. Limit equilibrium analysis (LEA) offers computational efficiency by simplifying slope stability problems into equilibrium equations, enabling faster calculations with reduced data input. FEM excels in accuracy for complex geometries, while LEA provides a pragmatic balance between computation speed and engineering precision for routine stability assessments.
Applicability to Complex Geological Conditions
Finite element modeling excels in handling complex geological conditions by simulating the nonlinear behavior and interactions of heterogeneous soil layers, fractures, and anisotropic materials with high precision. Limit equilibrium analysis, while simpler and computationally efficient, often assumes simplified geometries and homogeneous soil properties, limiting its accuracy in intricate stratigraphic settings or irregular failure surfaces. Therefore, finite element modeling provides a more robust framework for stability assessment in geologically complex scenarios such as fault zones, variable lithologies, and multidimensional stress distributions.
Case Studies: Real-World Applications and Outcomes
Finite element modeling (FEM) provides detailed stress-strain analysis in geotechnical engineering projects like tunnel excavation and slope stability, revealing deformation patterns and failure mechanisms beyond the scope of traditional methods. Limit equilibrium analysis (LEA) excels in practical case studies like landslide risk assessment and retaining wall design by offering rapid factor of safety calculations under varying loading conditions. Comparative case studies demonstrate FEM's superior accuracy in complex soil-structure interaction scenarios, while LEA remains preferred for preliminary design due to computational simplicity and regulatory acceptance.
Limitations and Challenges of Each Approach
Finite element modeling (FEM) faces challenges related to high computational cost and the need for detailed material properties, which can limit its practicality for large-scale geotechnical problems. Limit equilibrium analysis (LEA) struggles with assumptions of rigid soil behavior and simplified failure surfaces, potentially leading to less accurate stability predictions in complex conditions. Both methods require careful calibration and validation against field data to mitigate inherent limitations and ensure reliable results.
Future Trends in Slope Stability Analysis Techniques
Future trends in slope stability analysis techniques emphasize the integration of finite element modeling (FEM) with advanced limit equilibrium analysis (LEA) to enhance predictive accuracy and computational efficiency. Emerging developments include the application of machine learning algorithms to refine material property estimations within FEM and real-time monitoring data assimilation in LEA for dynamic slope behavior assessment. Increasing use of 3D modeling and probabilistic approaches aims to provide more comprehensive risk evaluations and optimize slope design under uncertain geological conditions.
Stress-strain distribution
Finite element modeling provides detailed stress-strain distribution analysis by simulating material behavior under loads, whereas limit equilibrium analysis simplifies calculations by focusing primarily on overall stability without capturing stress-strain variations within the soil mass.
Failure criteria
Finite element modeling uses advanced failure criteria like Mohr-Coulomb and Drucker-Prager to simulate stress-strain behavior and predict material failure, while limit equilibrium analysis relies on simplified shear strength parameters and factor of safety to evaluate slope stability and failure conditions.
Mesh discretization
Mesh discretization in finite element modeling involves dividing a structure into smaller elements to accurately simulate stress and deformation, while limit equilibrium analysis typically does not require mesh discretization as it focuses on overall stability using simplified slices or blocks.
Shear strength reduction
Shear strength reduction in finite element modeling provides a more detailed and continuous assessment of soil stability compared to the discrete slip surface approach used in limit equilibrium analysis.
Factor of safety (FoS)
Finite element modeling provides a detailed, stress-based Factor of Safety (FoS) assessment by simulating material behavior and failure modes, while limit equilibrium analysis calculates FoS using simplified force and moment balance equations for slope stability evaluation.
Plasticity modeling
Finite element modeling provides advanced plasticity modeling by simulating material behavior under complex stress conditions, whereas limit equilibrium analysis primarily assesses stability based on simplified equilibrium states without detailed plastic deformation representation.
Pore pressure coupling
Finite element modeling offers advanced pore pressure coupling capabilities for more accurate simulation of soil behavior compared to the simplified assumptions in limit equilibrium analysis.
Nonlinear material behavior
Finite element modeling accurately simulates nonlinear material behavior by capturing complex stress-strain relationships and deformation patterns, whereas limit equilibrium analysis assumes linear behavior and primarily evaluates overall stability without modeling material nonlinearity.
Slope stability simulation
Finite element modeling provides detailed stress-strain behavior and realistic deformation patterns for slope stability simulation, whereas limit equilibrium analysis estimates factor of safety through simplified force and moment equilibrium assumptions.
Constitutive models
Finite element modeling employs advanced constitutive models to accurately simulate material behavior under diverse conditions, whereas limit equilibrium analysis relies on simplified assumptions without detailed constitutive representations.
finite element modeling vs limit equilibrium analysis Infographic
 njnir.com
njnir.com