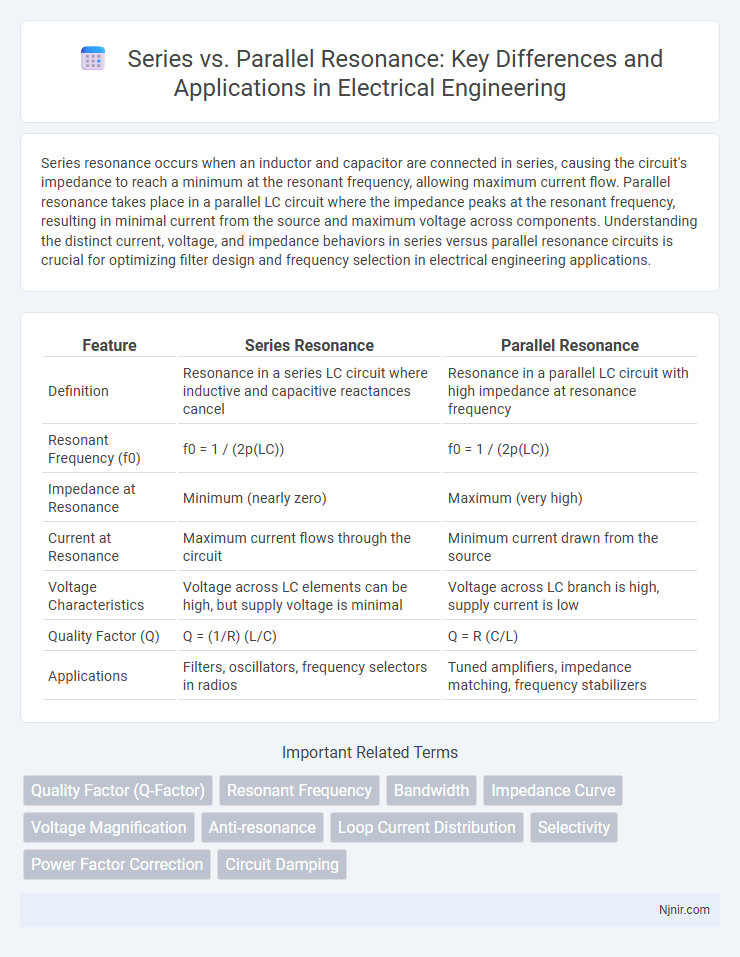
Series resonance occurs when an inductor and capacitor are connected in series, causing the circuit's impedance to reach a minimum at the resonant frequency, allowing maximum current flow. Parallel resonance takes place in a parallel LC circuit where the impedance peaks at the resonant frequency, resulting in minimal current from the source and maximum voltage across components. Understanding the distinct current, voltage, and impedance behaviors in series versus parallel resonance circuits is crucial for optimizing filter design and frequency selection in electrical engineering applications.
Table of Comparison
| Feature | Series Resonance | Parallel Resonance |
|---|---|---|
| Definition | Resonance in a series LC circuit where inductive and capacitive reactances cancel | Resonance in a parallel LC circuit with high impedance at resonance frequency |
| Resonant Frequency (f0) | f0 = 1 / (2p(LC)) | f0 = 1 / (2p(LC)) |
| Impedance at Resonance | Minimum (nearly zero) | Maximum (very high) |
| Current at Resonance | Maximum current flows through the circuit | Minimum current drawn from the source |
| Voltage Characteristics | Voltage across LC elements can be high, but supply voltage is minimal | Voltage across LC branch is high, supply current is low |
| Quality Factor (Q) | Q = (1/R) (L/C) | Q = R (C/L) |
| Applications | Filters, oscillators, frequency selectors in radios | Tuned amplifiers, impedance matching, frequency stabilizers |
Introduction to Resonance in Electrical Circuits
Resonance in electrical circuits occurs when the inductive reactance equals the capacitive reactance, causing the circuit to oscillate at its natural frequency. Series resonance involves a single path where impedance is minimized, resulting in maximum current flow, while parallel resonance features branches with maximum impedance and minimal current flow. Understanding resonance is essential for optimizing filter design, tuning circuits, and enhancing signal selectivity in radio frequency applications.
Fundamental Concepts: Series and Parallel Resonance
Series resonance occurs when the inductive reactance equals the capacitive reactance, causing the circuit's impedance to reach a minimum and the current to peak at the resonant frequency. Parallel resonance happens when the total current in the circuit is minimized as the inductive and capacitive currents cancel each other, resulting in maximum impedance at resonance. Both types of resonance are fundamental in analyzing AC circuits for frequency selection, impedance matching, and signal filtering applications.
Circuit Configurations and Key Differences
Series resonance occurs when inductive and capacitive reactances in a single loop cancel each other, resulting in minimum impedance and maximum current flow at the resonant frequency. Parallel resonance takes place in a circuit where inductive and capacitive branches are connected in parallel, causing maximum impedance and minimum current drawn from the source at resonance frequency. Key differences include the voltage and current behavior, with series resonance favoring high current and low impedance, while parallel resonance promotes high voltage across the branches and high impedance to the source.
Impedance Behavior in Series vs Parallel Resonance
In series resonance, impedance reaches its minimum value, as the inductive reactance and capacitive reactance cancel each other out, resulting in the circuit behaving like a pure resistor. Conversely, in parallel resonance, impedance reaches its maximum value due to the opposing currents through the inductor and capacitor reducing the overall current drawn from the source. This distinct impedance behavior makes series resonance ideal for current amplification and parallel resonance suitable for voltage amplification in AC circuit analysis.
Resonant Frequency: Calculations and Comparisons
Resonant frequency in series resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC), calculated by \( f_0 = \frac{1}{2\pi\sqrt{LC}} \), resulting in minimum impedance and maximum current. In parallel resonance, resonant frequency is the same formula \( f_0 = \frac{1}{2\pi\sqrt{LC}} \), but the circuit exhibits maximum impedance and minimum current at resonance. Comparing both, resonant frequency depends solely on inductance (L) and capacitance (C) values, while their impedance behaviors differ significantly, influencing circuit applications.
Quality Factor (Q-Factor) in Series and Parallel Circuits
The Quality Factor (Q-Factor) in series resonance circuits indicates the sharpness of the resonance peak, calculated as the ratio of inductive reactance to resistance, resulting in higher Q for lower resistance values. In parallel resonance circuits, the Q-Factor is defined by the ratio of resistance to the capacitive or inductive reactance, where higher resistance leads to increased Q, reflecting narrower bandwidth and higher selectivity. Understanding the different dependencies of Q-Factor on circuit elements in series and parallel configurations is essential for optimizing performance in filters, oscillators, and frequency-selective networks.
Voltage and Current Characteristics at Resonance
In series resonance, the circuit's impedance reaches a minimum, causing the current to peak while the voltage across individual components varies, with inductive and capacitive voltages canceling each other out. In parallel resonance, the impedance reaches a maximum, resulting in a minimum current drawn from the source, while voltage across the resonant branch is at its peak. Voltage magnification occurs in parallel resonance, whereas current magnification is characteristic of series resonance at the resonant frequency.
Applications of Series Resonant Circuits
Series resonant circuits are widely applied in radio frequency (RF) tuning, allowing selective frequency filtering to improve signal clarity in communication devices. They are essential in oscillators and amplifiers, providing high impedance at resonance that maximizes energy transfer and minimizes losses. In power systems, series resonance is utilized for harmonic filtering and impedance matching, enhancing the efficiency of electrical power transmission.
Applications of Parallel Resonant Circuits
Parallel resonant circuits are widely used in radio frequency (RF) applications such as oscillators, filters, and impedance matching networks due to their high selectivity and ability to block signal frequencies outside the resonant frequency. They are essential in tuning circuits of communication receivers and transmitters, providing stable frequency control with minimal signal loss. These circuits also find applications in voltage-controlled oscillators (VCOs) and sensor signal conditioning where precise frequency stabilization is required.
Series vs Parallel Resonance: Practical Considerations and Selection Criteria
Series resonance circuits exhibit minimum impedance at resonant frequency, making them ideal for applications requiring high current flow and precise frequency selection, such as filters and oscillators. Parallel resonance circuits offer maximum impedance at resonance, providing voltage amplification and noise rejection benefits, suitable for voltage-controlled oscillators and RF amplifiers. Selection criteria depend on factors like desired bandwidth, quality factor (Q), load impedance, and application-specific stability requirements.
Quality Factor (Q-Factor)
Series resonance circuits exhibit higher Quality Factors (Q-factors) due to lower energy losses compared to parallel resonance circuits, where the Q-factor depends heavily on the ratio of reactance to resistance.
Resonant Frequency
Series resonance occurs at the frequency where the inductive reactance equals the capacitive reactance, minimizing impedance and maximizing current, while parallel resonance happens at the frequency where the total admittance is minimized, resulting in maximum impedance and minimal current.
Bandwidth
Series resonance exhibits a narrow bandwidth due to its low resistance at resonance, while parallel resonance features a wider bandwidth because of higher circuit impedance.
Impedance Curve
Series resonance exhibits a sharp minimum impedance at the resonant frequency, while parallel resonance shows a sharp maximum impedance, clearly distinguishing their impedance curves.
Voltage Magnification
Series resonance exhibits voltage magnification close to the supply voltage, whereas parallel resonance produces a significantly higher voltage magnification across the resonant circuit components.
Anti-resonance
Anti-resonance occurs in parallel resonance circuits when the circuit impedance peaks, causing current to minimize and voltage to maximize at a specific frequency.
Loop Current Distribution
Series resonance occurs when the loop current distribution maximizes current flow due to minimal impedance, while parallel resonance leads to current division that minimizes loop currents by maximizing impedance within the circuit.
Selectivity
Series resonance exhibits lower selectivity due to a narrower bandwidth, whereas parallel resonance offers higher selectivity with a sharper frequency response peak.
Power Factor Correction
Series resonance minimizes impedance at resonance frequency, improving power factor by maximizing current flow, while parallel resonance maximizes impedance, enhancing power factor correction by reducing reactive power in AC circuits.
Circuit Damping
Series resonance circuits exhibit minimal damping due to low resistance causing high current peaks, while parallel resonance circuits have higher damping from increased effective resistance, resulting in narrower bandwidth and lower current amplitude.
Series vs Parallel Resonance Infographic
 njnir.com
njnir.com