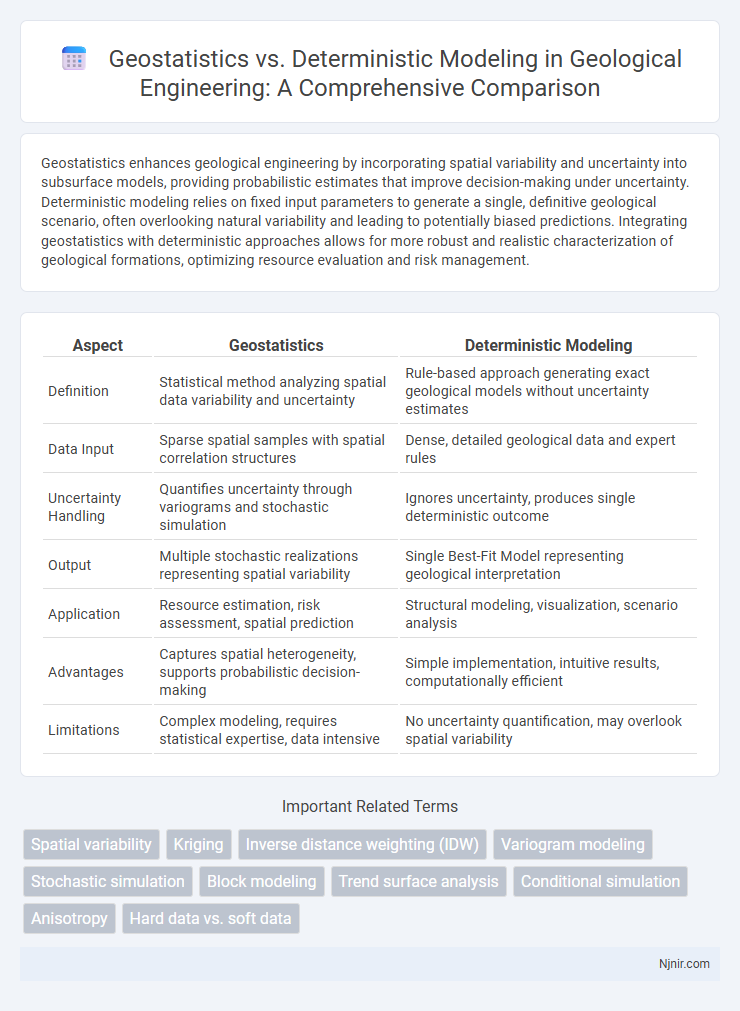
Geostatistics enhances geological engineering by incorporating spatial variability and uncertainty into subsurface models, providing probabilistic estimates that improve decision-making under uncertainty. Deterministic modeling relies on fixed input parameters to generate a single, definitive geological scenario, often overlooking natural variability and leading to potentially biased predictions. Integrating geostatistics with deterministic approaches allows for more robust and realistic characterization of geological formations, optimizing resource evaluation and risk management.
Table of Comparison
| Aspect | Geostatistics | Deterministic Modeling |
|---|---|---|
| Definition | Statistical method analyzing spatial data variability and uncertainty | Rule-based approach generating exact geological models without uncertainty estimates |
| Data Input | Sparse spatial samples with spatial correlation structures | Dense, detailed geological data and expert rules |
| Uncertainty Handling | Quantifies uncertainty through variograms and stochastic simulation | Ignores uncertainty, produces single deterministic outcome |
| Output | Multiple stochastic realizations representing spatial variability | Single Best-Fit Model representing geological interpretation |
| Application | Resource estimation, risk assessment, spatial prediction | Structural modeling, visualization, scenario analysis |
| Advantages | Captures spatial heterogeneity, supports probabilistic decision-making | Simple implementation, intuitive results, computationally efficient |
| Limitations | Complex modeling, requires statistical expertise, data intensive | No uncertainty quantification, may overlook spatial variability |
Introduction to Geostatistics and Deterministic Modeling
Geostatistics employs probabilistic methods to analyze spatially correlated data, enabling accurate predictions of variable distributions across geographic areas. Deterministic modeling relies on established physical laws and fixed input parameters to generate precise, repeatable outcomes without incorporating spatial uncertainty. Understanding these foundational approaches allows for informed selection of modeling techniques based on the nature of data and required prediction accuracy.
Fundamental Concepts in Geostatistics
Geostatistics relies on probabilistic models and spatial statistics to analyze and predict spatially correlated data, emphasizing variance, covariance, and spatial continuity through tools like semivariograms. Deterministic modeling, in contrast, uses fixed, non-probabilistic inputs to generate predictions, often ignoring spatial uncertainty and variability inherent in geological data. Fundamental concepts in geostatistics include spatial dependence, stationarity, and the use of kriging for optimal unbiased spatial estimation, which enhances decision-making in resource evaluation and environmental studies.
Core Principles of Deterministic Modeling
Deterministic modeling relies on fixed input parameters and physical laws to produce precise, repeatable results without accounting for uncertainty, ensuring predictable system behavior based on established equations and boundary conditions. Core principles include the use of mathematical relationships to describe processes, defined initial and boundary conditions, and the assumption that system responses are entirely determined by these inputs. This method contrasts with geostatistics, which incorporates spatial variability and stochastic processes to handle uncertainty and heterogeneity in data.
Data Requirements in Geostatistical and Deterministic Approaches
Geostatistical modeling requires extensive spatially correlated data points to accurately estimate and predict variable distributions, leveraging variograms to quantify spatial continuity. Deterministic modeling relies on fewer, often non-spatially referenced data inputs, using predefined rules or equations to simulate system behavior without inherently addressing spatial variability. The effectiveness of geostatistics depends heavily on data density and spatial distribution, whereas deterministic models prioritize data quality and theoretical relationships over spatial data quantity.
Spatial Interpolation: Kriging vs. Inverse Distance Weighting
Spatial interpolation in geostatistics primarily uses Kriging, which incorporates spatial autocorrelation and provides unbiased, minimum-variance estimates by modeling the variogram structure of the dataset. In contrast, deterministic modeling with Inverse Distance Weighting (IDW) assigns weights solely based on the inverse distance from known points without accounting for spatial correlation, often resulting in smoother but less accurate surfaces. Kriging's ability to quantify estimation variance makes it superior for uncertainty assessment compared to IDW's heuristic approach.
Handling Uncertainty: Probabilistic vs. Exact Models
Geostatistics employs probabilistic models to handle uncertainty by incorporating spatial variability and quantifying prediction errors through statistical distributions. Deterministic modeling provides exact values based on fixed input parameters, offering no explicit measure of uncertainty. This fundamental difference makes geostatistics more suitable for risk assessment and decision-making under uncertain conditions.
Applications in Geological Engineering Projects
Geostatistics enhances geological engineering projects by providing probabilistic models that account for spatial variability in subsurface properties, improving resource estimation accuracy and risk assessment in mining and groundwater studies. Deterministic modeling offers precise, rule-based simulations for geological structures, commonly applied in tunnel design and slope stability analysis where clear geological boundaries are essential. Combining geostatistics with deterministic approaches optimizes decision-making by integrating uncertainty quantification with detailed geological predictions.
Strengths and Limitations of Geostatistical Methods
Geostatistical methods excel in quantifying spatial variability and uncertainty by using probabilistic models such as kriging, which provides unbiased estimations and measures of prediction error. These techniques effectively incorporate spatial correlation structures derived from variograms, enhancing the accuracy of resource estimation in mining, environmental science, and hydrology. Limitations include high computational demands, sensitivity to the quality of input data and variogram modeling, and challenges in handling non-stationary or highly heterogeneous datasets.
Deterministic Modeling: Advantages and Constraints
Deterministic modeling offers precise predictions by relying on fixed input parameters and mathematical equations, ensuring consistent and repeatable outcomes essential for engineering and environmental applications. It simplifies complex systems by assuming known variables, which enhances computational efficiency and clarity in interpretation. However, deterministic models often lack the ability to account for natural variability and spatial uncertainty, limiting their effectiveness in heterogeneous or poorly sampled geological settings compared to geostatistical approaches.
Selecting the Appropriate Approach for Geological Engineering
Selecting between geostatistics and deterministic modeling in geological engineering depends on data variability and project objectives. Geostatistics excels in capturing spatial uncertainty and heterogeneity through probabilistic methods like kriging, making it ideal for resource estimation and risk assessment. Deterministic modeling provides explicit, simplified representations suitable for structural analysis and scenarios with limited data variability or when a single, clear outcome is needed.
Spatial variability
Geostatistics quantifies spatial variability using probabilistic models and spatial correlations while deterministic modeling assumes fixed spatial patterns without inherent variability.
Kriging
Kriging in geostatistics provides spatially optimized, probabilistic predictions by modeling spatial correlation, unlike deterministic modeling which generates fixed values without quantifying uncertainty.
Inverse distance weighting (IDW)
Inverse distance weighting (IDW) in geostatistics estimates unknown values by averaging nearby measured points weighted inversely by distance, contrasting with deterministic modeling's fixed mathematical relationships.
Variogram modeling
Variogram modeling in geostatistics captures spatial dependence and variability more effectively than deterministic modeling by quantifying spatial autocorrelation through semivariance functions.
Stochastic simulation
Stochastic simulation in geostatistics captures spatial variability and uncertainty by generating multiple equally probable realizations, whereas deterministic modeling provides a single best-estimate solution without accounting for uncertainty.
Block modeling
Block modeling in geostatistics incorporates spatial variability and uncertainty for more accurate resource estimation, whereas deterministic modeling relies on fixed input values, often oversimplifying geological heterogeneity.
Trend surface analysis
Trend surface analysis in geostatistics models spatial variability by fitting polynomial functions to data trends, providing more accurate spatial predictions than deterministic modeling's fixed, non-probabilistic approaches.
Conditional simulation
Conditional simulation in geostatistics generates multiple equally probable spatial realizations by incorporating data uncertainty, unlike deterministic modeling which provides a single fixed estimate without accounting for spatial variability.
Anisotropy
Geostatistics captures spatial anisotropy by modeling direction-dependent variability with variograms, while deterministic modeling often assumes isotropy or applies simplified anisotropic parameters without accounting for spatial correlation structures.
Hard data vs. soft data
Hard data in geostatistics provides quantitative measurements with spatial correlation, whereas deterministic modeling often relies on soft data such as expert judgment or qualitative inputs for predictions.
geostatistics vs deterministic modeling Infographic
 njnir.com
njnir.com