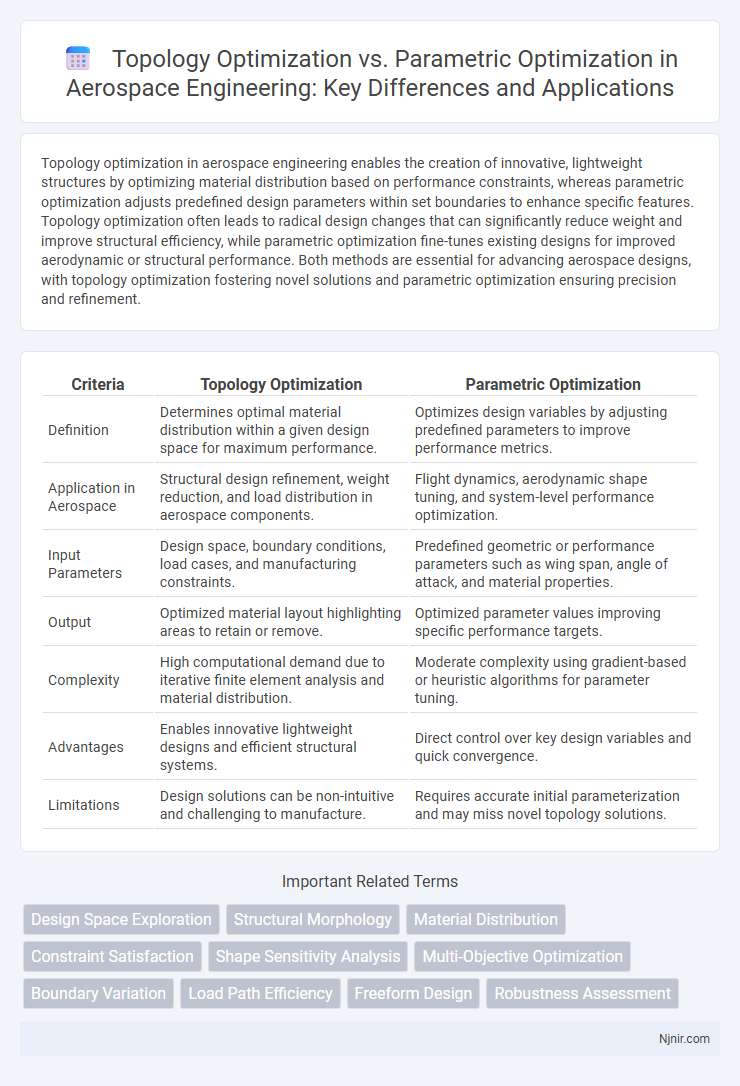
Topology optimization in aerospace engineering enables the creation of innovative, lightweight structures by optimizing material distribution based on performance constraints, whereas parametric optimization adjusts predefined design parameters within set boundaries to enhance specific features. Topology optimization often leads to radical design changes that can significantly reduce weight and improve structural efficiency, while parametric optimization fine-tunes existing designs for improved aerodynamic or structural performance. Both methods are essential for advancing aerospace designs, with topology optimization fostering novel solutions and parametric optimization ensuring precision and refinement.
Table of Comparison
| Criteria | Topology Optimization | Parametric Optimization |
|---|---|---|
| Definition | Determines optimal material distribution within a given design space for maximum performance. | Optimizes design variables by adjusting predefined parameters to improve performance metrics. |
| Application in Aerospace | Structural design refinement, weight reduction, and load distribution in aerospace components. | Flight dynamics, aerodynamic shape tuning, and system-level performance optimization. |
| Input Parameters | Design space, boundary conditions, load cases, and manufacturing constraints. | Predefined geometric or performance parameters such as wing span, angle of attack, and material properties. |
| Output | Optimized material layout highlighting areas to retain or remove. | Optimized parameter values improving specific performance targets. |
| Complexity | High computational demand due to iterative finite element analysis and material distribution. | Moderate complexity using gradient-based or heuristic algorithms for parameter tuning. |
| Advantages | Enables innovative lightweight designs and efficient structural systems. | Direct control over key design variables and quick convergence. |
| Limitations | Design solutions can be non-intuitive and challenging to manufacture. | Requires accurate initial parameterization and may miss novel topology solutions. |
Introduction to Topology and Parametric Optimization
Topology optimization focuses on determining the optimal material layout within a given design space to maximize performance objectives such as weight reduction or structural stiffness. Parametric optimization involves adjusting design variables systematically within predefined parameters to improve performance outcomes across various scenarios. Both methods leverage computational algorithms but address different aspects of the design process: topology optimization refines the physical structure, while parametric optimization fine-tunes the design parameters.
Fundamental Principles of Topology Optimization
Topology optimization fundamentally involves distributing material within a given design space to achieve the best structural performance based on specific constraints and load conditions. It utilizes mathematical algorithms to iteratively remove inefficient material, emphasizing stiffness or weight reduction while maintaining strength and functionality. Unlike parametric optimization, which adjusts design variables within predefined geometries, topology optimization explores the optimal layout without initial shape limitations, enabling innovative and highly efficient structural designs.
Core Concepts of Parametric Optimization
Parametric optimization involves systematically adjusting design variables to achieve the best performance based on specific objective functions, such as minimizing weight or maximizing efficiency. This method relies on predefined parameters and uses algorithms to explore a range of values, ensuring the design meets constraints and performance targets. Core concepts include sensitivity analysis, gradient-based search, and iterative refinement, enabling precise control over design outcomes in complex engineering problems.
Comparative Overview: Topology vs Parametric Optimization
Topology optimization focuses on material distribution within a given design space to achieve optimal structural performance, often used in engineering fields like aerospace and automotive industries. Parametric optimization involves adjusting design variables and parameters to improve performance, relying on predefined design spaces and relationships, commonly applied in architectural and mechanical designs. While topology optimization excels in creating novel, lightweight structures, parametric optimization provides precise control over specific design attributes, making them complementary in advanced design processes.
Applications in Aerospace Structure Design
Topology optimization enables aerospace engineers to identify the most efficient material layout within a given design space, significantly reducing weight while maintaining structural integrity and performance under complex load conditions. Parametric optimization fine-tunes critical design variables such as wing geometry, structural thickness, and material properties to enhance aerodynamic efficiency, fuel consumption, and durability. Combining topology and parametric optimization in aerospace structure design results in lightweight, high-performance components that meet strict regulatory standards and operational demands in aircraft and spacecraft development.
Computational Methods and Tools
Topology optimization employs finite element analysis and gradient-based algorithms to iteratively remove inefficient material, enabling the design of lightweight structures with optimal stress distribution. Parametric optimization utilizes design variables within parametric models, leveraging techniques like genetic algorithms, surrogate modeling, and response surface methodology to explore complex design spaces systematically. Computational tools such as ANSYS, Abaqus, and COMSOL Multiphysics support topology optimization, while CAD-integrated platforms like Grasshopper and MATLAB with optimization toolboxes excel in parametric optimization workflows.
Impact on Weight Reduction and Performance
Topology optimization achieves substantial weight reduction by strategically redistributing material within a design space to maximize structural efficiency while maintaining performance criteria. Parametric optimization fine-tunes predefined design variables to enhance performance metrics but may yield less dramatic weight savings compared to topology-driven methodologies. Combining both approaches can lead to optimal lightweight structures with improved mechanical behavior in aerospace, automotive, and civil engineering applications.
Design Constraints and Manufacturing Considerations
Topology optimization excels in defining optimal material distribution within given design constraints, often leading to complex geometries that maximize structural performance but may challenge traditional manufacturing methods like casting or machining. Parametric optimization focuses on adjusting predefined geometric parameters to meet design constraints while maintaining manufacturability, making it suitable for designs with tighter manufacturing tolerances and specific production requirements. Manufacturing considerations heavily influence the choice between these methods, as topology optimization may require advanced fabrication techniques like additive manufacturing, whereas parametric optimization aligns well with standard processes due to its parameter-driven design approach.
Case Studies in Aerospace Engineering
Case studies in aerospace engineering reveal topology optimization excels in redesigning structural components for weight reduction while maintaining strength, directly impacting fuel efficiency and load capacity. Parametric optimization focuses on tuning design variables such as wing geometry and control surfaces, optimizing aerodynamic performance and stability. Combining both methods in aerospace applications maximizes performance gains by refining internal structure and external shape concurrently.
Future Trends and Innovations
Topology optimization is advancing through integration with artificial intelligence and machine learning, enabling more efficient and adaptive material distribution in complex designs. Parametric optimization is evolving with real-time data analytics and cloud computing, allowing for dynamic adjustment of design parameters to meet specific performance criteria under varying conditions. Future trends indicate a convergence of these methods, leveraging hybrid algorithms to achieve optimal solutions that balance structural integrity, cost-efficiency, and sustainability.
Design Space Exploration
Topology Optimization maximizes material efficiency by iteratively refining structural layouts within a broad design space, while Parametric Optimization systematically explores variable parameters to identify optimal solutions within defined design boundaries.
Structural Morphology
Topology optimization reshapes structural morphology by defining optimal material distribution within a design space, while parametric optimization adjusts predefined geometric parameters to enhance structural performance.
Material Distribution
Topology optimization maximizes structural performance by optimizing material distribution within a design space, while parametric optimization adjusts predefined design parameters without directly altering material layout.
Constraint Satisfaction
Topology optimization excels at satisfying complex structural constraints by optimizing material layout within a design space, while parametric optimization efficiently handles predefined geometric constraints by adjusting parameter values to meet performance goals.
Shape Sensitivity Analysis
Shape sensitivity analysis in topology optimization evaluates structural performance changes by altering geometric boundaries, whereas parametric optimization adjusts predefined design variables to improve system efficiency.
Multi-Objective Optimization
Multi-objective topology optimization simultaneously refines material distribution and structural layout to achieve optimal performance metrics, while parametric optimization adjusts predefined design variables to balance multiple objectives such as weight, strength, and cost.
Boundary Variation
Topology optimization enhances boundary variation by systematically removing material to achieve optimal structural layouts, whereas parametric optimization adjusts predefined boundary parameters to refine design performance within set constraints.
Load Path Efficiency
Topology optimization maximizes load path efficiency by strategically distributing material to minimize stress concentrations, whereas parametric optimization adjusts design variables within predefined shapes to improve performance but may overlook global load path improvements.
Freeform Design
Freeform design leverages topology optimization to create material-efficient structures by defining optimal material distribution, while parametric optimization refines shape and performance through adjustable design variables within predefined constraints.
Robustness Assessment
Topology optimization enhances structural robustness by minimizing stress concentrations through material distribution, while parametric optimization improves robustness by fine-tuning design variables within defined ranges to accommodate uncertainties.
Topology Optimization vs Parametric Optimization Infographic
 njnir.com
njnir.com