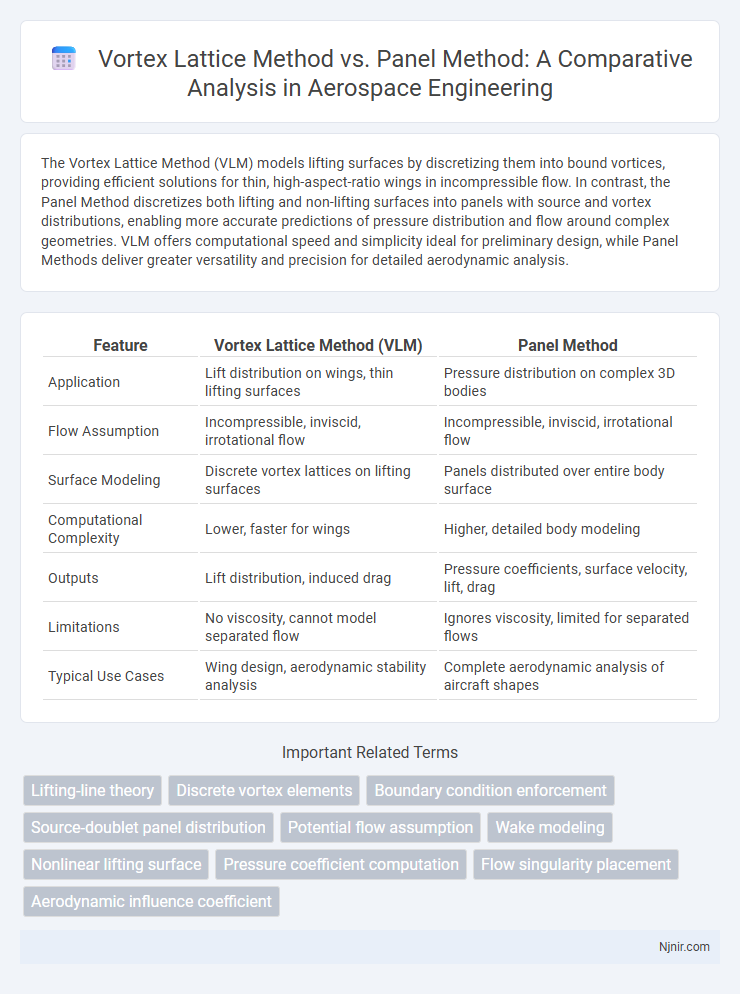
The Vortex Lattice Method (VLM) models lifting surfaces by discretizing them into bound vortices, providing efficient solutions for thin, high-aspect-ratio wings in incompressible flow. In contrast, the Panel Method discretizes both lifting and non-lifting surfaces into panels with source and vortex distributions, enabling more accurate predictions of pressure distribution and flow around complex geometries. VLM offers computational speed and simplicity ideal for preliminary design, while Panel Methods deliver greater versatility and precision for detailed aerodynamic analysis.
Table of Comparison
| Feature | Vortex Lattice Method (VLM) | Panel Method |
|---|---|---|
| Application | Lift distribution on wings, thin lifting surfaces | Pressure distribution on complex 3D bodies |
| Flow Assumption | Incompressible, inviscid, irrotational flow | Incompressible, inviscid, irrotational flow |
| Surface Modeling | Discrete vortex lattices on lifting surfaces | Panels distributed over entire body surface |
| Computational Complexity | Lower, faster for wings | Higher, detailed body modeling |
| Outputs | Lift distribution, induced drag | Pressure coefficients, surface velocity, lift, drag |
| Limitations | No viscosity, cannot model separated flow | Ignores viscosity, limited for separated flows |
| Typical Use Cases | Wing design, aerodynamic stability analysis | Complete aerodynamic analysis of aircraft shapes |
Introduction to Aerodynamic Modeling Techniques
The Vortex Lattice Method (VLM) and Panel Method are fundamental aerodynamic modeling techniques used to predict lift, drag, and flow characteristics around aircraft surfaces. VLM relies on discretizing lifting surfaces into a lattice of bound vortices, simplifying the calculation of lift distribution with high computational efficiency for incompressible, inviscid flows. Panel Method incorporates both source and vortex panels to model potential flow around complex geometries, providing more detailed pressure distribution and accommodating thicker airfoils but at increased computational cost.
Fundamentals of the Vortex Lattice Method (VLM)
The Vortex Lattice Method (VLM) models lifting surfaces by discretizing them into a grid of horseshoe vortices to simulate aerodynamic lift distribution, relying on potential flow theory and enforcing boundary conditions on control points. VLM computes the circulation strength of each vortex element to satisfy the no-penetration condition, predicting lift and induced drag with moderate computational efficiency compared to the Panel Method. Unlike the Panel Method, which solves for surface pressures using singularity distributions and can handle arbitrary geometries, VLM specializes in thin, planar wings and offers a streamlined approach for linear aerodynamic analysis.
Basics of the Panel Method in Aerodynamics
The Panel Method in aerodynamics models the flow around a body by discretizing its surface into small panels with singularity elements like sources and vortices, enabling the calculation of velocity potential and pressure distribution. Unlike the Vortex Lattice Method, which primarily uses bound vortices on lifting surfaces for lift estimation, the Panel Method can handle both lifting and non-lifting bodies and accounts for complex geometries including thickness effects. This boundary element approach solves integral equations based on potential flow theory, making it versatile for analyzing aerodynamic characteristics such as pressure coefficients and aerodynamic forces.
Mathematical Foundations: VLM vs Panel Method
The Vortex Lattice Method (VLM) relies on discretizing lifting surfaces into a lattice of bound vortices combined with trailing vortices to solve for lifting flow using potential flow theory and the Biot-Savart law. In contrast, the Panel Method uses surface panels with prescribed boundary conditions to solve Laplace's equation for the velocity potential, incorporating both source and vortex distributions to model the flow over the body. VLM is primarily suited for thin wings with small angles of attack, emphasizing lift prediction, while Panel Methods provide more flexibility to handle complex geometries and capture pressure distributions, relying on integral equations derived from potential flow theory.
Assumptions and Limitations of Each Method
The Vortex Lattice Method assumes a thin, lifting surface with linear aerodynamics and incompressible, inviscid flow, limiting its accuracy in predicting viscous effects and strong nonlinear behaviors such as flow separation. The Panel Method models potential flow around arbitrary shapes by discretizing surfaces into panels, but it assumes inviscid, irrotational, and incompressible flow, which neglects viscous drag and cannot capture boundary layer phenomena. Both methods are limited in high angle of attack scenarios and cannot accurately simulate complex three-dimensional turbulent flows or compressibility effects at transonic and supersonic speeds.
Computational Efficiency and Resource Requirements
The Vortex Lattice Method (VLM) offers superior computational efficiency compared to Panel Methods due to its simplified representation of lifting surfaces using discrete vortex lines, reducing the number of unknowns and matrix size. Panel Methods require denser surface discretization, increasing computational resources and memory usage significantly, especially for complex geometries with nonlinear flow features. VLM is advantageous for preliminary aerodynamic analyses where lower computational cost and faster runtimes are critical, while Panel Methods provide higher fidelity at the expense of increased computational load.
Accuracy in Predicting Lift and Drag Forces
The Vortex Lattice Method (VLM) provides efficient and reasonably accurate predictions of lift forces on lifting surfaces by modeling bound vortices along the wing span but lacks direct drag estimation due to its inviscid flow assumptions. In contrast, the Panel Method models both potential flow and surface panels, allowing for better approximation of pressure distribution and form drag, leading to more accurate drag force predictions. Combining VLM for lift with supplementary drag models or employing Panel Methods yields improved overall aerodynamic force accuracy in computational simulations.
Applicability to Different Aerospace Configurations
The Vortex Lattice Method (VLM) is highly effective for analyzing thin, lifting surfaces such as wings and tailplanes, making it ideal for conventional fixed-wing aircraft and high-aspect-ratio configurations. The Panel Method, offering a more general approach by modeling both lifting and non-lifting surfaces, accommodates complex geometries including fuselages, blended wing bodies, and multi-component systems. VLM excels in rapid aerodynamic predictions for preliminary design, while the Panel Method provides detailed flow solutions essential for unconventional or integrated aerospace configurations.
Case Studies: Practical Aerospace Applications
Case studies comparing Vortex Lattice Method (VLM) and Panel Method in aerospace reveal VLM excels in analyzing lift distribution and induced drag for wings with simple geometries, commonly applied in preliminary wing design phases. Panel Method demonstrates superior accuracy in capturing complex flow phenomena around complete aircraft configurations, including fuselage and control surfaces, making it ideal for detailed aerodynamic assessments. Practical applications show VLM's computational efficiency benefits iterative design processes, whereas Panel Method's comprehensive flow modeling supports final validation and optimization stages.
Future Trends in Aerodynamic Simulation Techniques
Future trends in aerodynamic simulation techniques emphasize enhanced computational efficiency and accuracy through hybrid approaches combining Vortex Lattice Method (VLM) and Panel Method elements. Integration of machine learning algorithms with these traditional methods aims to accelerate convergence and improve predictive capabilities for complex flow phenomena. Increasing use of high-performance computing enables real-time simulations, fostering advanced aircraft design and optimization.
Lifting-line theory
The Vortex Lattice Method improves upon Lifting-line theory by modeling three-dimensional wing aerodynamics with a discrete grid of horseshoe vortices, while the Panel Method uses surface panels to solve potential flow, providing detailed pressure distribution but requiring more computational resources.
Discrete vortex elements
The Vortex Lattice Method models aerodynamic surfaces using discrete vortex elements arranged in a lattice to efficiently compute lift distribution, whereas the Panel Method employs distributed source and vortex panels for more versatile but computationally intensive potential flow analysis.
Boundary condition enforcement
The Vortex Lattice Method enforces boundary conditions by satisfying flow tangency on discrete horseshoe vortices along lifting surfaces, whereas the Panel Method applies boundary conditions more precisely on surface panels by directly imposing flow tangency at control points to model both lifting and non-lifting surfaces.
Source-doublet panel distribution
The Vortex Lattice Method models lifting surfaces using discrete vortex horseshoe elements while the Panel Method employs source-doublet panel distributions to accurately represent potential flow around complex geometries.
Potential flow assumption
Vortex Lattice Method models lifting surfaces using discrete vortex lines under the potential flow assumption of inviscid, incompressible, and irrotational flow, while Panel Method employs distributed sources and vortices on body surfaces to solve potential flow around complex geometries more accurately.
Wake modeling
The Vortex Lattice Method models the wake using discrete trailing vortices that simulate induced velocities and wake effects more accurately than the Panel Method, which typically employs simpler, steady wake assumptions.
Nonlinear lifting surface
The Vortex Lattice Method efficiently approximates nonlinear lifting surfaces by discretizing them into horseshoe vortices, while the Panel Method provides more accurate pressure distributions by solving boundary integral equations on surface panels for complex nonlinear aerodynamic flows.
Pressure coefficient computation
The Vortex Lattice Method computes pressure coefficients using discrete vortex strengths on lifting surfaces, while the Panel Method calculates them by solving source and vortex distributions on surface panels to capture both lifting and non-lifting flows more accurately.
Flow singularity placement
Vortex Lattice Method places flow singularities as discrete vortices on the lifting surfaces, while Panel Method distributes flow singularities as source and vortex panels over the surface to model both lifting and non-lifting flows accurately.
Aerodynamic influence coefficient
The Vortex Lattice Method offers a computationally efficient approach to estimate aerodynamic influence coefficients by modeling lifting surfaces with discrete horseshoe vortices, while the Panel Method provides increased accuracy through surface discretization and potential flow solutions but demands greater computational resources.
Vortex Lattice Method vs Panel Method Infographic
 njnir.com
njnir.com