Phase margin measures the stability of a control system by indicating how much the phase can change before the system becomes unstable, while gain margin quantifies the allowable gain increase before instability occurs. A higher phase margin generally implies better transient response and robustness, whereas sufficient gain margin ensures the system can tolerate variations in system gain without oscillations. Both margins are critical in frequency response analysis to design and tune stable and reliable electrical control systems.
Table of Comparison
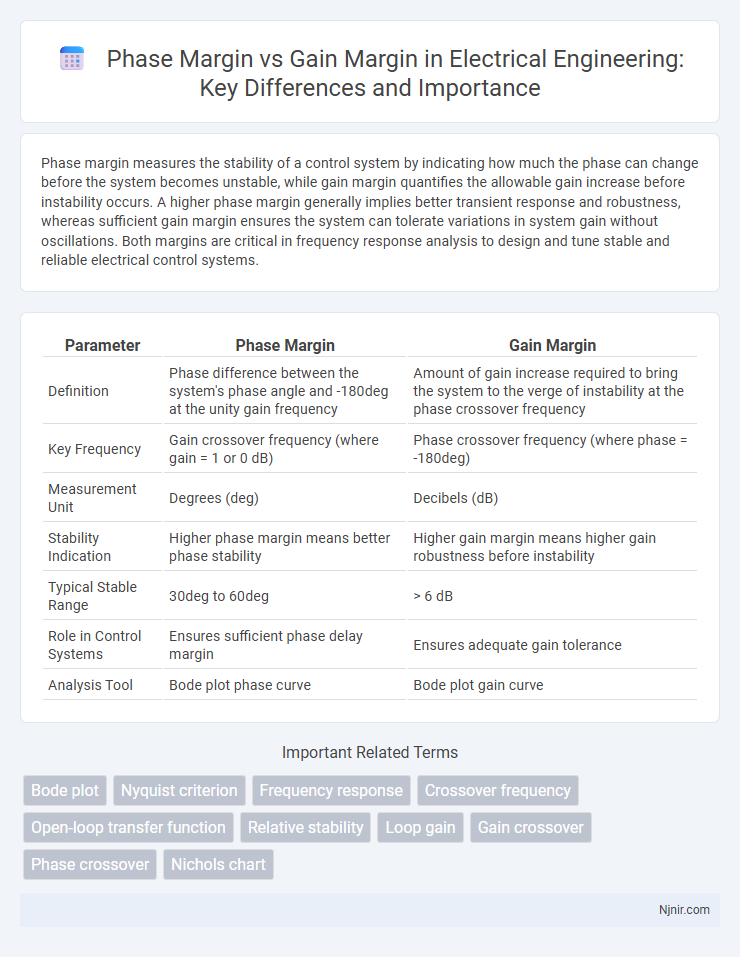
| Parameter | Phase Margin | Gain Margin |
|---|---|---|
| Definition | Phase difference between the system's phase angle and -180deg at the unity gain frequency | Amount of gain increase required to bring the system to the verge of instability at the phase crossover frequency |
| Key Frequency | Gain crossover frequency (where gain = 1 or 0 dB) | Phase crossover frequency (where phase = -180deg) |
| Measurement Unit | Degrees (deg) | Decibels (dB) |
| Stability Indication | Higher phase margin means better phase stability | Higher gain margin means higher gain robustness before instability |
| Typical Stable Range | 30deg to 60deg | > 6 dB |
| Role in Control Systems | Ensures sufficient phase delay margin | Ensures adequate gain tolerance |
| Analysis Tool | Bode plot phase curve | Bode plot gain curve |
Introduction to Stability in Electrical Engineering
Phase margin and gain margin are critical parameters for assessing the stability of control systems in electrical engineering. Phase margin quantifies the additional phase lag required to bring the system to the verge of instability at the gain crossover frequency, while gain margin measures the factor by which gain can increase before the system becomes unstable at the phase crossover frequency. Both margins provide essential insights into the robustness of feedback systems, enabling engineers to design stable and reliable electrical circuits.
Understanding Phase Margin
Phase margin measures the difference in phase angle between a system's open-loop response and -180 degrees at the gain crossover frequency, indicating stability robustness. A higher phase margin implies greater tolerance to system variations before oscillations occur, while a low or negative phase margin signals potential instability. Understanding phase margin is crucial for designing controllers that maintain a stable feedback loop in control systems.
Exploring Gain Margin
Gain margin measures the stability buffer by quantifying how much the system gain can increase before it reaches the critical point of instability, typically expressed in decibels (dB). It is determined from the frequency response plot by identifying the gain increase required to bring the phase shift to -180 degrees at the crossover frequency. Unlike phase margin, which assesses phase safety, gain margin specifically focuses on the allowable amplitude increase, making it crucial for designing robust control systems that can tolerate gain variations without becoming unstable.
Mathematical Definitions: Phase Margin vs Gain Margin
Phase margin is defined as the difference between the phase angle of a system's open-loop transfer function at the gain crossover frequency and -180 degrees, mathematically expressed as PM = 180deg + G(jo_gc), where o_gc is the frequency where |G(jo)| = 1. Gain margin quantifies the allowable gain increase before instability, calculated as GM = 1/|G(jo_pc)|, where o_pc is the phase crossover frequency at which the phase angle equals -180 degrees. Both margins provide key stability metrics derived from the frequency response characteristics of the system using Nyquist or Bode plots.
Importance of Stability Margins in Circuit Design
Stability margins, including phase margin and gain margin, are critical parameters in circuit design that quantify how close a system is to oscillation or instability. Phase margin measures the additional phase lag required to bring the system to the verge of oscillation at the gain crossover frequency, while gain margin indicates how much gain increase will cause instability at the phase crossover frequency. Ensuring adequate stability margins enhances the reliability and performance of amplifiers, control systems, and feedback circuits by preventing undesired oscillations and maintaining predictable operation.
Phase Margin Interpretation in Bode Plots
Phase margin in Bode plots represents the additional phase lag required to bring the system to the verge of instability, measured at the gain crossover frequency where the magnitude is unity (0 dB). A larger phase margin indicates a more stable control system with better tolerance to gain variations and external disturbances. Engineers utilize phase margin to assess system robustness, ensuring sufficient delay margins to prevent oscillatory or unstable responses.
Gain Margin Analysis Using Frequency Response
Gain margin analysis using frequency response measures the stability of a control system by determining how much gain can increase before the system becomes unstable, typically identified at the phase crossover frequency where the phase angle is -180 degrees. This margin is quantified as the reciprocal of the gain at this frequency, expressed in decibels, indicating the buffer against oscillation onset. Accurate gain margin assessment through frequency response aids in designing robust controllers by ensuring sufficient tolerance to gain variations without compromising system stability.
Comparing the Effects on System Performance
Phase margin and gain margin are critical indicators of system stability and performance in control systems. A higher phase margin typically improves system resilience to oscillations and enhances transient response, whereas a larger gain margin ensures robustness against variations in system gain without causing instability. Balancing phase margin and gain margin is essential for optimizing stability, minimizing overshoot, and achieving desired damping characteristics in feedback control loops.
Common Mistakes in Evaluating Stability Margins
Confusing phase margin with gain margin is a common mistake, as phase margin measures the additional phase lag required to bring the system to the verge of instability, while gain margin quantifies how much gain can increase before instability occurs. Another frequent error is neglecting to evaluate margins at the correct crossover frequencies; phase margin should be assessed at the gain crossover frequency where the magnitude equals unity, and gain margin at the phase crossover frequency where the phase is -180 degrees. Misinterpreting negative phase margin or gain margin values as stable indicators often leads to incorrect stability assessments, resulting in design failures or oscillatory system behavior.
Practical Applications and Design Guidelines
Phase margin and gain margin are critical parameters in control system stability analysis, directly influencing the robustness and responsiveness of feedback loops. Practical applications in industrial automation emphasize maintaining a phase margin of at least 45 degrees and a gain margin above 6 dB to ensure adequate damping and avoid oscillations under varying load conditions. Design guidelines recommend using these margins to tune PID controllers and compensate for model uncertainties, enhancing system reliability and performance in real-world environments.
Bode plot
Phase margin measures stability by indicating how much phase shift can increase before a system becomes unstable at gain crossover frequency, while gain margin quantifies how much gain can increase before instability at phase crossover frequency on a Bode plot.
Nyquist criterion
Phase margin and gain margin quantify system stability by measuring the distance from the critical point (-1,0) on the Nyquist plot, with phase margin representing the additional phase lag required to reach -180 degrees at unity gain and gain margin indicating how much gain can increase before instability occurs.
Frequency response
Phase margin measures the additional phase lag required to reach instability at the gain crossover frequency, while gain margin quantifies the allowable gain increase before instability occurs at the phase crossover frequency in a system's frequency response.
Crossover frequency
Phase margin at the crossover frequency indicates system stability by measuring the phase lag at the gain crossover point, while gain margin quantifies the allowable gain increase before instability.
Open-loop transfer function
Phase margin measures the additional phase lag required to reach instability at the unity gain frequency, while gain margin quantifies the allowable gain increase before instability, both derived from the open-loop transfer function's frequency response.
Relative stability
Phase margin and gain margin are critical indicators of relative stability in control systems, with higher values generally indicating increased robustness against oscillations and system instability.
Loop gain
Loop gain critically influences phase margin and gain margin by determining system stability margins, where higher loop gain generally reduces phase margin and affects gain margin thresholds.
Gain crossover
The gain margin measures system stability by indicating how much gain can increase before instability at the gain crossover frequency, where the phase shift is -180 degrees.
Phase crossover
Phase margin measures the stability buffer at the gain crossover frequency, while gain margin quantifies stability at the phase crossover frequency where the phase shift is -180 degrees.
Nichols chart
The Nichols chart visually represents the relationship between phase margin and gain margin by plotting open-loop gain and phase data, where the phase margin corresponds to the horizontal distance from the -180deg phase line to the crossover frequency, and the gain margin corresponds to the vertical distance from the 0 dB gain line to the phase crossover frequency.
phase margin vs gain margin Infographic
 njnir.com
njnir.com