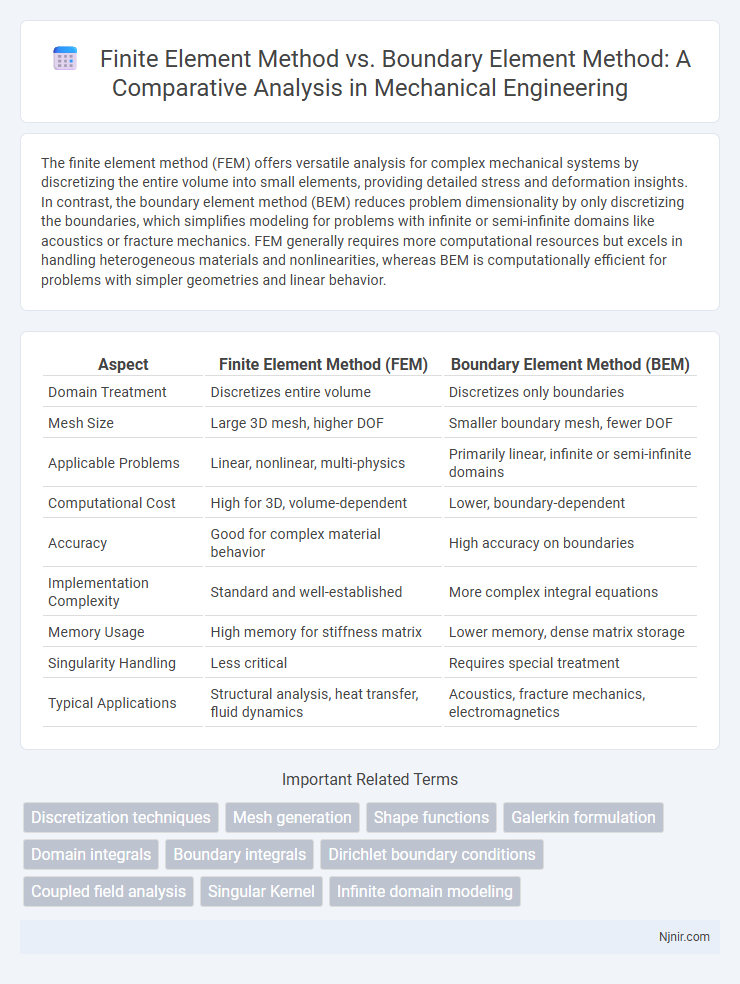
The finite element method (FEM) offers versatile analysis for complex mechanical systems by discretizing the entire volume into small elements, providing detailed stress and deformation insights. In contrast, the boundary element method (BEM) reduces problem dimensionality by only discretizing the boundaries, which simplifies modeling for problems with infinite or semi-infinite domains like acoustics or fracture mechanics. FEM generally requires more computational resources but excels in handling heterogeneous materials and nonlinearities, whereas BEM is computationally efficient for problems with simpler geometries and linear behavior.
Table of Comparison
| Aspect | Finite Element Method (FEM) | Boundary Element Method (BEM) |
|---|---|---|
| Domain Treatment | Discretizes entire volume | Discretizes only boundaries |
| Mesh Size | Large 3D mesh, higher DOF | Smaller boundary mesh, fewer DOF |
| Applicable Problems | Linear, nonlinear, multi-physics | Primarily linear, infinite or semi-infinite domains |
| Computational Cost | High for 3D, volume-dependent | Lower, boundary-dependent |
| Accuracy | Good for complex material behavior | High accuracy on boundaries |
| Implementation Complexity | Standard and well-established | More complex integral equations |
| Memory Usage | High memory for stiffness matrix | Lower memory, dense matrix storage |
| Singularity Handling | Less critical | Requires special treatment |
| Typical Applications | Structural analysis, heat transfer, fluid dynamics | Acoustics, fracture mechanics, electromagnetics |
Introduction to Numerical Methods in Mechanical Engineering
Finite Element Method (FEM) discretizes the entire domain into smaller elements, enabling the analysis of complex geometries and heterogeneous materials in mechanical engineering problems. Boundary Element Method (BEM) reduces the problem to boundary discretization, significantly decreasing dimensionality and computational effort for linear, homogeneous domains. Numerical methods in mechanical engineering leverage FEM for detailed internal analysis and BEM for efficiency in solving problems involving infinite or semi-infinite domains.
Fundamentals of the Finite Element Method (FEM)
The Finite Element Method (FEM) divides a complex structure into smaller, simpler parts called finite elements, enabling precise numerical solutions to partial differential equations governing physical phenomena. FEM's fundamental process involves discretizing the domain, formulating element equations based on variational principles, and assembling a global system to approximate field variables like displacement or temperature. Compared to the Boundary Element Method (BEM), FEM requires volumetric meshing, offering greater flexibility in modeling heterogeneous materials and nonlinear problems but often at higher computational costs.
Fundamentals of the Boundary Element Method (BEM)
The Boundary Element Method (BEM) fundamentally transforms partial differential equations into boundary integral equations, reducing problem dimensionality by focusing only on surface discretization compared to the domain discretization required by the Finite Element Method (FEM). BEM efficiently handles infinite or semi-infinite domains commonly found in acoustics, electromagnetics, and fluid dynamics by utilizing fundamental solutions or Green's functions. This approach minimizes computational effort for problems with complex boundaries but requires careful treatment of singular integrals and is generally more suitable for linear problems.
Mathematical Formulation: FEM vs. BEM
Finite Element Method (FEM) involves discretizing the entire problem domain into smaller subdomains or elements, using variational methods to convert partial differential equations into a system of algebraic equations. Boundary Element Method (BEM) reduces the problem dimensionality by formulating integral equations only on the domain boundaries, relying on Green's functions for fundamental solutions. FEM requires volume meshing and results in sparse matrices while BEM uses boundary meshing, producing dense matrices but potentially lowering computational costs for problems with infinite or semi-infinite domains.
Mesh Generation and Model Preparation
Finite Element Method (FEM) requires volumetric mesh generation, subdividing the entire domain into elements such as tetrahedrons or hexahedrons, which can be computationally intensive for complex geometries. Boundary Element Method (BEM) only necessitates discretizing the problem boundary into surface elements, significantly reducing mesh complexity and preparation time. Mesh generation in BEM offers advantages for problems involving infinite domains or stress analysis where boundary conditions dominate, while FEM provides versatility for nonlinear and heterogeneous material modeling.
Computational Efficiency and Resource Requirements
Finite Element Method (FEM) typically demands higher computational resources and memory due to volumetric meshing of complex geometries, leading to increased processing time especially in 3D problems. Boundary Element Method (BEM) reduces dimensionality by only discretizing boundaries, resulting in fewer elements and lower memory usage, which enhances computational efficiency for problems with infinite or semi-infinite domains. However, BEM involves dense matrix systems that can challenge solver performance, making FEM more scalable for large-scale problems with heterogeneous materials.
Applicability to Different Mechanical Engineering Problems
The finite element method (FEM) excels in solving complex structural, thermal, and fluid mechanics problems with intricate geometries and material behaviors by discretizing the entire domain. The boundary element method (BEM) is particularly effective for problems involving infinite or semi-infinite domains, such as acoustics, elasticity, and potential flow, by discretizing only the boundaries, reducing dimensionality and computational effort. FEM offers greater versatility for nonlinear, heterogeneous, and multi-physics simulations, whereas BEM is favored for linear problems with simpler material properties but complex boundary conditions.
Accuracy and Solution Quality Comparison
The finite element method (FEM) provides high accuracy in solving complex, nonlinear, and heterogeneous problems by discretizing the entire domain, capturing detailed internal behavior. The boundary element method (BEM) excels in problems with infinite or semi-infinite domains by only discretizing boundaries, often enhancing accuracy for external problems while reducing dimensionality. FEM typically offers superior solution quality for volumetric and inhomogeneous materials, whereas BEM can achieve comparable accuracy with fewer elements in boundary-dominated scenarios.
Advantages and Limitations of FEM and BEM
Finite Element Method (FEM) offers high flexibility in modeling complex geometries and heterogeneous materials, making it ideal for structural, thermal, and fluid analyses, but it requires volumetric meshing, which can increase computational cost for large domains. Boundary Element Method (BEM) reduces problem dimensionality by only discretizing boundaries, leading to fewer elements and faster computation for infinite or semi-infinite domains, yet it struggles with non-linear problems and requires fundamental solutions that limit applicability. FEM is well-suited for non-linear, dynamic, and multi-physics problems with detailed internal behavior, while BEM excels in problems with simple boundaries and homogeneous materials but is less effective in handling complex internal regions and non-linearities.
Future Trends in Numerical Methods for Mechanical Engineers
The finite element method (FEM) continues to advance with enhanced mesh refinement techniques and integration of machine learning algorithms for more accurate stress and deformation predictions in complex mechanical systems. Boundary element method (BEM) developments focus on reducing computational cost through improved fundamental solution algorithms and hybrid approaches that couple BEM with FEM to address multi-scale problems efficiently. Future trends emphasize leveraging high-performance computing and artificial intelligence to optimize numerical simulations, enabling mechanical engineers to solve increasingly intricate and multidisciplinary engineering challenges with greater precision.
Discretization techniques
Finite Element Method discretizes the entire domain into small volumetric elements, whereas Boundary Element Method discretizes only the boundary, reducing dimensionality and computational effort in problems with infinite or semi-infinite domains.
Mesh generation
Finite Element Method requires volumetric mesh generation over the entire domain, whereas Boundary Element Method only needs surface mesh generation, significantly reducing mesh complexity and computational effort.
Shape functions
Finite element method utilizes polynomial shape functions within elements for approximating solutions, whereas boundary element method employs fundamental solutions as shape functions exclusively on boundaries, reducing dimensionality and computational effort.
Galerkin formulation
The Galerkin formulation in the finite element method discretizes the entire domain into elements optimizing solution accuracy, whereas in the boundary element method, it reduces problem dimensionality by discretizing only the boundary, enhancing computational efficiency for infinite or semi-infinite domains.
Domain integrals
The finite element method efficiently solves domain integrals by discretizing the entire volume, whereas the boundary element method reduces problem complexity by transforming domain integrals into boundary integrals, minimizing dimensionality.
Boundary integrals
The Boundary Element Method reduces problem dimensionality by formulating boundary integrals only on surfaces, whereas the Finite Element Method requires volume discretization for domain integrals.
Dirichlet boundary conditions
The finite element method efficiently handles Dirichlet boundary conditions by directly applying prescribed values on nodes, whereas the boundary element method reduces the problem to boundary integrals but requires special treatment to enforce Dirichlet conditions accurately.
Coupled field analysis
Finite Element Method excels in detailed internal coupled field analysis of complex structures, while Boundary Element Method efficiently handles infinite domains with reduced dimensional discretization in coupled field problems.
Singular Kernel
The finite element method discretizes the entire domain while the boundary element method specifically addresses singular kernels by formulating integral equations over boundaries, improving accuracy in problems with singularities.
Infinite domain modeling
The Boundary Element Method efficiently models infinite domain problems by reducing dimensionality and accurately representing far-field behavior, unlike the Finite Element Method which requires artificial truncation of the domain.
finite element method vs boundary element method Infographic
 njnir.com
njnir.com