Stress in mechanical engineering represents the internal force per unit area within materials subjected to external loads, while strain measures the material's deformation response to that applied stress. The relationship between stress and strain is fundamental in determining a material's elasticity, yielding point, and overall mechanical behavior under various loading conditions. Understanding this interaction enables engineers to design structures and components that can withstand specific forces without failure.
Table of Comparison
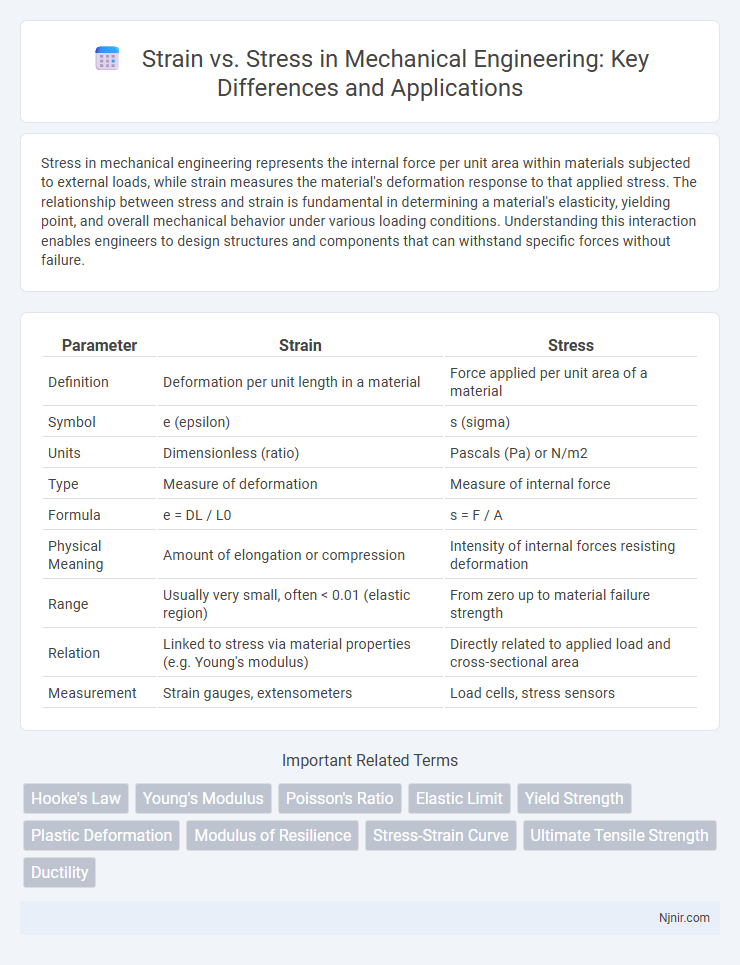
| Parameter | Strain | Stress |
|---|---|---|
| Definition | Deformation per unit length in a material | Force applied per unit area of a material |
| Symbol | e (epsilon) | s (sigma) |
| Units | Dimensionless (ratio) | Pascals (Pa) or N/m2 |
| Type | Measure of deformation | Measure of internal force |
| Formula | e = DL / L0 | s = F / A |
| Physical Meaning | Amount of elongation or compression | Intensity of internal forces resisting deformation |
| Range | Usually very small, often < 0.01 (elastic region) | From zero up to material failure strength |
| Relation | Linked to stress via material properties (e.g. Young's modulus) | Directly related to applied load and cross-sectional area |
| Measurement | Strain gauges, extensometers | Load cells, stress sensors |
Introduction to Strain and Stress in Mechanical Engineering
Strain and stress are fundamental concepts in mechanical engineering that describe how materials respond to applied forces. Stress quantifies the internal force per unit area within a material, measured in pascals (Pa), while strain represents the deformation or displacement relative to the material's original length, expressed as a dimensionless ratio. Understanding the relationship between strain and stress is critical for designing structures that withstand mechanical loads without failure.
Fundamental Definitions: What is Stress?
Stress is a measure of internal forces exerted per unit area within a material, typically expressed in pascals (Pa). It quantifies how external loads, such as tension, compression, or shear, distribute throughout an object's cross-sectional area. Stress helps predict material behavior under applied forces, playing a critical role in mechanical engineering and materials science.
Understanding Strain: Types and Measurement
Strain represents the deformation experienced by a material when subjected to stress, categorized primarily into tensile, compressive, and shear strain based on the nature of the applied force. Measurement of strain involves quantifying the change in length or shape relative to the original dimensions, commonly using strain gauges or extensometers for precise data acquisition. Understanding these types and measurement methods is critical for analyzing material behavior under load and predicting failure in engineering applications.
Stress-Strain Relationship: Theoretical Perspectives
The stress-strain relationship describes how materials deform under applied forces, quantified by stress (force per unit area) and strain (deformation per original length). Hooke's Law theoretically models this relationship in the elastic region, where stress is proportional to strain with the constant of proportionality defined as the material's modulus of elasticity. Beyond the elastic limit, nonlinear models such as plasticity theory characterize permanent deformation, reflecting complex material behavior through stress-strain curves.
Hooke’s Law and Elastic Behavior
Hooke's Law defines the linear relationship between stress and strain within the elastic limit of a material, expressed as s = Ee, where s represents stress, e represents strain, and E is the modulus of elasticity. Elastic behavior refers to the material's ability to return to its original shape after the removal of stress, provided the stress does not exceed the elastic limit. The proportionality between stress and strain under Hooke's Law is fundamental to predicting material deformation and designing mechanical components for durability.
Plastic Deformation and Yield Point
Plastic deformation occurs when a material undergoes irreversible strain beyond its elastic limit, characterized by permanent atomic dislocation rearrangements. The yield point marks the transition from elastic behavior to plastic deformation, indicating the stress level at which materials begin to deform plastically. Understanding the yield point is crucial for predicting structural failure and designing materials with specific strength and ductility properties.
Stress-Strain Curves: Interpretation and Analysis
Stress-strain curves graphically represent the relationship between stress and strain, essential for understanding material behavior under load. Key points include the elastic region, where deformation is reversible, and the yield point, marking the transition to plastic deformation. Analysis of these curves provides critical data such as elastic modulus, yield strength, ultimate tensile strength, and fracture point, enabling engineers to predict material performance and failure modes.
Factors Affecting Stress and Strain in Materials
Stress and strain in materials are influenced by factors such as the type of material, temperature, and the rate of applied load. Material properties like elasticity, ductility, and grain structure determine how stress is distributed and how much deformation (strain) occurs under load. Environmental conditions, including humidity and corrosion, can also alter the material's strength and ability to withstand stress without permanent deformation.
Practical Applications of Stress and Strain Concepts
Understanding the relationship between stress and strain is crucial in engineering design to ensure structural integrity and prevent material failure. Stress, defined as the force applied per unit area, helps determine the load-bearing capacity of materials used in bridges, buildings, and machinery. Strain, representing the deformation resulting from stress, aids in predicting material behavior under real-world conditions, enabling safer and more efficient construction and manufacturing processes.
Significance of Stress vs. Strain in Engineering Design
Stress represents the internal force per unit area within materials, critical for predicting failure points in engineering components, while strain measures the deformation or displacement resulting from applied stress. Understanding the relationship between stress and strain enables engineers to select appropriate materials and design structures that withstand operational loads without excessive deformation or failure. Accurate analysis of stress versus strain curves informs safety factors and ensures durability and reliability in mechanical and structural applications.
Hooke's Law
Hooke's Law states that strain is directly proportional to stress within the elastic limit of a material, expressed as s = Ee, where s is stress, e is strain, and E is the material's modulus of elasticity.
Young's Modulus
Young's Modulus quantifies the linear relationship between stress and strain, representing the stiffness of a material under elastic deformation.
Poisson's Ratio
Poisson's ratio quantifies the negative ratio of transverse to axial strain in a material subjected to uniaxial stress, serving as a key parameter for understanding elastic deformation behavior.
Elastic Limit
The elastic limit defines the maximum stress a material can withstand without undergoing permanent strain or deformation.
Yield Strength
Yield strength is the critical stress level at which a material undergoes permanent strain, marking the transition from elastic deformation to plastic deformation in the stress-strain curve.
Plastic Deformation
Plastic deformation occurs when a material undergoes strain beyond its elastic limit under applied stress, causing permanent molecular or dislocation movement.
Modulus of Resilience
Modulus of Resilience quantifies the maximum energy per unit volume a material can elastically absorb under strain before yielding under stress.
Stress-Strain Curve
The stress-strain curve graphically represents the relationship between the applied stress and resulting strain, illustrating material properties such as elasticity, yield strength, and ultimate tensile strength.
Ultimate Tensile Strength
Ultimate Tensile Strength (UTS) represents the maximum stress a material withstands while being stretched before failure, distinguishing it from strain, which measures deformation relative to original length.
Ductility
Ductility is a material's ability to undergo significant plastic strain before fracture, distinguishing strain as a measure of deformation from stress, which quantifies the internal force causing that deformation.
strain vs stress Infographic
 njnir.com
njnir.com