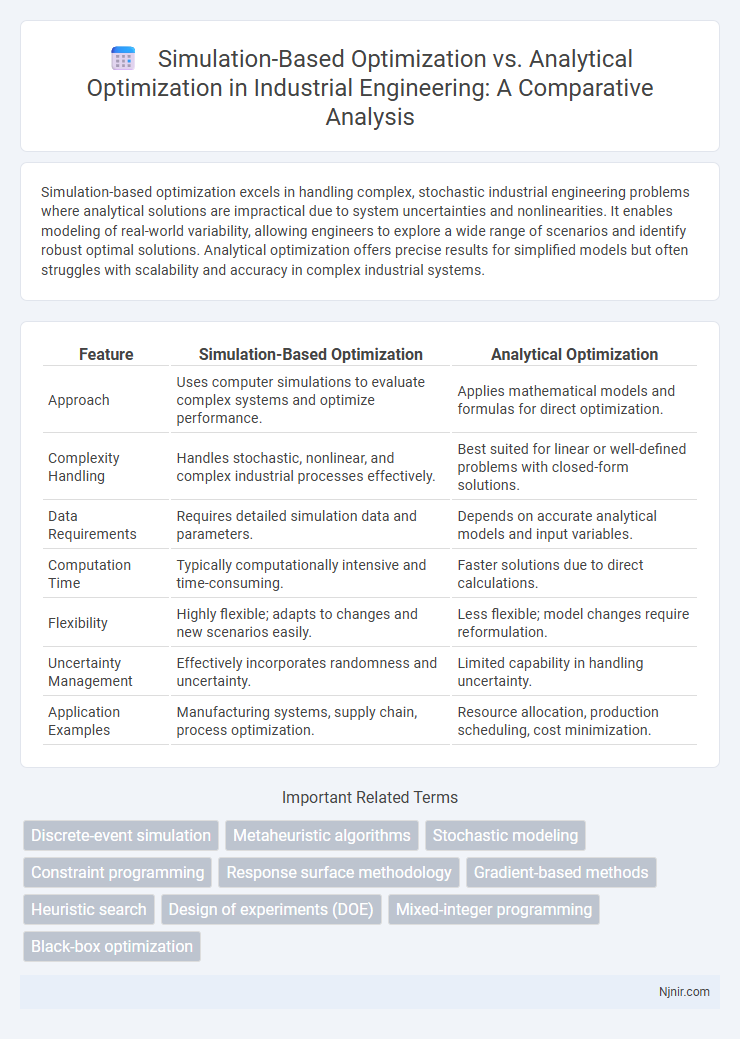
Simulation-based optimization excels in handling complex, stochastic industrial engineering problems where analytical solutions are impractical due to system uncertainties and nonlinearities. It enables modeling of real-world variability, allowing engineers to explore a wide range of scenarios and identify robust optimal solutions. Analytical optimization offers precise results for simplified models but often struggles with scalability and accuracy in complex industrial systems.
Table of Comparison
| Feature | Simulation-Based Optimization | Analytical Optimization |
|---|---|---|
| Approach | Uses computer simulations to evaluate complex systems and optimize performance. | Applies mathematical models and formulas for direct optimization. |
| Complexity Handling | Handles stochastic, nonlinear, and complex industrial processes effectively. | Best suited for linear or well-defined problems with closed-form solutions. |
| Data Requirements | Requires detailed simulation data and parameters. | Depends on accurate analytical models and input variables. |
| Computation Time | Typically computationally intensive and time-consuming. | Faster solutions due to direct calculations. |
| Flexibility | Highly flexible; adapts to changes and new scenarios easily. | Less flexible; model changes require reformulation. |
| Uncertainty Management | Effectively incorporates randomness and uncertainty. | Limited capability in handling uncertainty. |
| Application Examples | Manufacturing systems, supply chain, process optimization. | Resource allocation, production scheduling, cost minimization. |
Overview of Simulation-Based Optimization in Industrial Engineering
Simulation-based optimization in industrial engineering leverages computer models to evaluate complex systems under varying conditions, enabling decision-makers to identify optimal solutions when analytical methods are infeasible due to system complexity or uncertainty. It integrates simulation models with optimization algorithms such as genetic algorithms, particle swarm optimization, or simulated annealing to enhance system performance and resource utilization. This approach is particularly valuable for addressing stochastic, nonlinear, and multi-objective problems in manufacturing, supply chain management, and production scheduling.
Fundamentals of Analytical Optimization Methods
Analytical optimization methods rely on mathematical models and calculus-based techniques to find exact solutions by optimizing explicit objective functions under defined constraints. These methods involve techniques such as linear programming, nonlinear optimization, and convex analysis to determine optimal decision variables analytically. Unlike simulation-based optimization, analytical approaches require precise knowledge of problem structure and are effective for problems with well-defined mathematical formulations.
Key Differences Between Simulation-Based and Analytical Approaches
Simulation-based optimization uses computational models to mimic real-world processes and evaluate solutions under uncertainty, making it suitable for complex systems with stochastic elements. Analytical optimization relies on mathematical formulas and closed-form solutions to find optimal results, which is efficient for problems with well-defined, deterministic relationships. Key differences include simulation's ability to handle variability and randomness, while analytical methods provide exact solutions but often require simplifying assumptions.
Applicability of Simulation-Based Optimization in Complex Systems
Simulation-based optimization is particularly effective for complex systems where analytical models are difficult to formulate or solve due to nonlinearities, uncertainties, or high-dimensional decision spaces. It enables the evaluation of system performance under various scenarios by integrating simulation models with optimization algorithms, allowing for realistic representation and exploration of dynamic behaviors. This approach is widely applicable in fields such as manufacturing, logistics, and finance, where system complexity and stochastic variability hinder traditional analytical optimization methods.
Strengths and Limitations of Analytical Optimization
Analytical optimization excels in providing precise, mathematically rigorous solutions when the problem structure is well-defined with linear or convex models, enabling exact optimality guarantees. Its limitations arise from difficulties handling complex, nonlinear, or stochastic systems where assumptions such as differentiability and convexity do not hold, restricting applicability in real-world scenarios. Computational efficiency is high for small to medium-sized problems but deteriorates significantly with increasing dimensionality and model complexity, reducing practicality for large-scale or highly intricate optimization tasks.
Integration of Simulation and Analytical Methods
Simulation-based optimization leverages computational models to evaluate complex systems under uncertainty, while analytical optimization applies mathematical techniques for precise problem-solving. Integrating simulation and analytical methods enhances decision-making by combining the accuracy of mathematical models with the flexibility of simulation to address stochastic and dynamic system behaviors. This hybrid approach improves solution quality in fields such as manufacturing, logistics, and finance by optimizing under realistic constraints and variability.
Case Studies: Real-World Industrial Applications
Simulation-based optimization excels in complex industrial scenarios such as manufacturing scheduling at General Motors, where dynamic constraints and stochastic variables are prevalent, enabling adaptive decision-making through iterative simulations. Analytical optimization proves effective in supply chain management at companies like Amazon by providing closed-form solutions for deterministic models, optimizing inventory levels and logistics costs efficiently. Case studies reveal simulation-based methods offer flexibility for systems with uncertainty, whereas analytical approaches enable rapid, exact solutions in well-defined environments.
Computational Requirements and Efficiency Comparison
Simulation-based optimization demands significant computational resources due to iterative scenario evaluations and stochastic modeling, often requiring high-performance computing environments. Analytical optimization benefits from closed-form solutions or gradient-based methods, enabling faster convergence and lower computational overhead. When efficiency is paramount, analytical approaches outperform simulations in speed, though simulations offer flexibility in modeling complex, nonlinear systems.
Decision-Making Under Uncertainty: Simulation vs Analytical Optimization
Simulation-based optimization enables decision-making under uncertainty by modeling complex systems with stochastic variables, providing insights through scenario analysis and probabilistic outcomes. Analytical optimization relies on mathematical formulas and deterministic models to find optimal solutions, offering precise but often simplified decision frameworks. Combining both methods can enhance decision quality by leveraging simulation's flexibility and analytical accuracy in uncertain environments.
Future Trends in Optimization Techniques for Industrial Engineering
Simulation-based optimization integrates complex, real-world uncertainties and dynamic system behaviors, making it essential for predictive maintenance and adaptive manufacturing systems in industrial engineering. Analytical optimization relies on mathematical models and closed-form solutions, offering rapid decision-making for linear and convex problems but facing limitations with high-dimensional and stochastic systems. Future trends emphasize hybrid approaches combining machine learning with simulation and analytical methods to enhance scalability, accuracy, and real-time optimization in Industry 4.0 applications.
Discrete-event simulation
Simulation-based optimization using discrete-event simulation models complex stochastic systems with dynamic interactions for realistic performance evaluation, while analytical optimization relies on mathematical formulations and closed-form solutions, offering faster computation but less flexibility in modeling intricate system behaviors.
Metaheuristic algorithms
Metaheuristic algorithms excel in simulation-based optimization by efficiently exploring complex, nonlinear problem spaces where analytical optimization struggles with exact solutions due to model simplifications and computational constraints.
Stochastic modeling
Simulation-based optimization effectively handles stochastic modeling by using iterative computational experiments to evaluate complex probabilistic systems, whereas analytical optimization relies on mathematical formulations and closed-form solutions often limited to simpler stochastic assumptions.
Constraint programming
Constraint programming enhances simulation-based optimization by efficiently handling complex combinatorial constraints often impractical for traditional analytical optimization methods.
Response surface methodology
Response Surface Methodology enhances simulation-based optimization by efficiently modeling complex system responses, enabling precise identification of optimal conditions where analytical optimization is impractical or infeasible.
Gradient-based methods
Gradient-based methods in simulation-based optimization handle complex, stochastic systems by approximating gradients numerically, whereas analytical optimization relies on exact gradient calculations from explicit mathematical models.
Heuristic search
Heuristic search in simulation-based optimization efficiently explores complex solution spaces by iteratively improving candidate solutions, unlike analytical optimization which relies on exact mathematical models for problem-solving.
Design of experiments (DOE)
Simulation-based optimization uses Design of Experiments (DOE) to systematically explore complex, nonlinear systems by generating experimental data through simulations, while Analytical optimization relies on mathematical models and DOE primarily for identifying parameter sensitivities and optimal settings within deterministic frameworks.
Mixed-integer programming
Mixed-integer programming enables precise analytical optimization by solving mathematical models with discrete and continuous variables, while simulation-based optimization uses iterative simulations to evaluate complex system behaviors and stochastic uncertainties not easily captured by analytical methods.
Black-box optimization
Simulation-based optimization excels in solving black-box optimization problems by efficiently exploring complex, nonlinear systems without explicit analytical models, unlike analytical optimization which requires precise mathematical formulations.
Simulation-based optimization vs Analytical optimization Infographic
 njnir.com
njnir.com