Finite Element Analysis (FEA) primarily addresses structural mechanics by discretizing solid components to evaluate stress, strain, and deformation under various load conditions. Computational Fluid Dynamics (CFD) focuses on simulating fluid flow, heat transfer, and related phenomena by solving Navier-Stokes equations within defined fluid domains. Both methods are critical in mechanical engineering but differ in application scope, with FEA optimizing structural integrity and CFD enhancing fluid interaction performance.
Table of Comparison
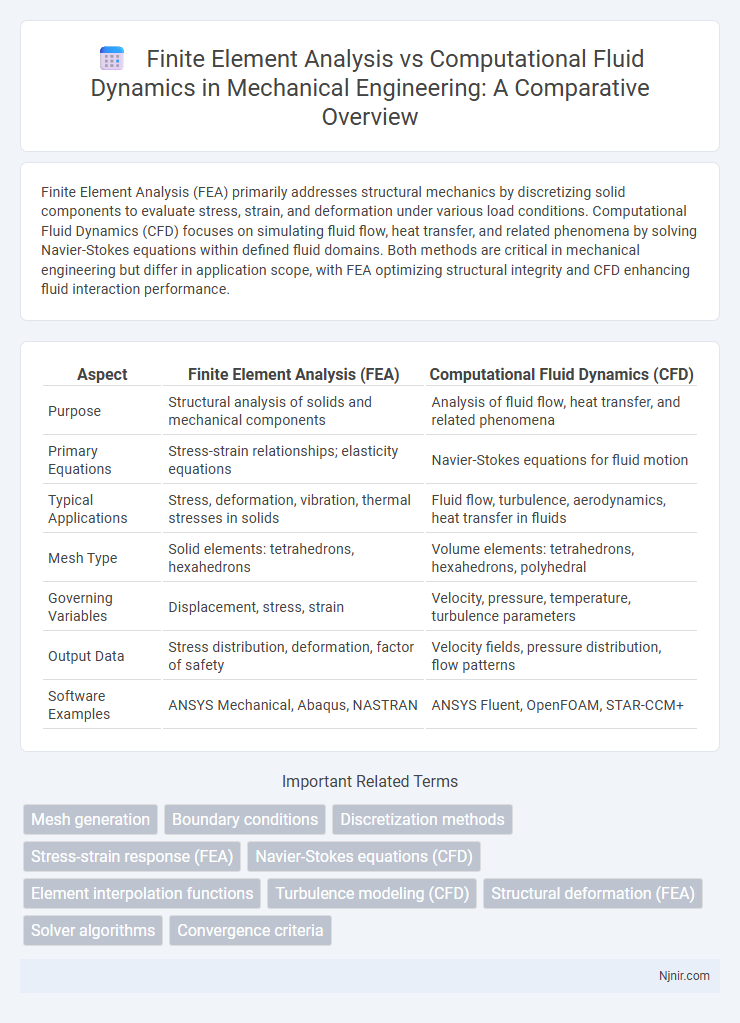
| Aspect | Finite Element Analysis (FEA) | Computational Fluid Dynamics (CFD) |
|---|---|---|
| Purpose | Structural analysis of solids and mechanical components | Analysis of fluid flow, heat transfer, and related phenomena |
| Primary Equations | Stress-strain relationships; elasticity equations | Navier-Stokes equations for fluid motion |
| Typical Applications | Stress, deformation, vibration, thermal stresses in solids | Fluid flow, turbulence, aerodynamics, heat transfer in fluids |
| Mesh Type | Solid elements: tetrahedrons, hexahedrons | Volume elements: tetrahedrons, hexahedrons, polyhedral |
| Governing Variables | Displacement, stress, strain | Velocity, pressure, temperature, turbulence parameters |
| Output Data | Stress distribution, deformation, factor of safety | Velocity fields, pressure distribution, flow patterns |
| Software Examples | ANSYS Mechanical, Abaqus, NASTRAN | ANSYS Fluent, OpenFOAM, STAR-CCM+ |
Introduction to Finite Element Analysis (FEA) and Computational Fluid Dynamics (CFD)
Finite Element Analysis (FEA) employs numerical methods to predict how structures respond to forces, heat, and vibration by dividing complex geometries into smaller elements for stress and deformation analysis. Computational Fluid Dynamics (CFD) simulates fluid flow, heat transfer, and related phenomena by solving Navier-Stokes equations within discretized fluid domains. Both techniques are essential in engineering for optimizing designs, with FEA focusing on solid mechanics and CFD specializing in fluid behavior.
Fundamental Principles of FEA
Finite element analysis (FEA) is based on the fundamental principle of discretizing a complex structure into smaller, manageable elements to solve physical problems mathematically. Each element's behavior is described by differential equations representing equilibrium, compatibility, and material constitutive relationships. This method enables accurate stress, strain, and deformation predictions in solid mechanics by approximating continuous fields through piecewise polynomial functions.
Core Concepts of CFD
Computational fluid dynamics (CFD) centers on solving the Navier-Stokes equations to simulate fluid flow and heat transfer within complex geometries, utilizing numerical methods like finite volume or finite difference for discretization. Core concepts include turbulence modeling, mesh generation, and boundary condition specification, which directly affect solution accuracy and convergence. Unlike finite element analysis (FEA) that primarily focuses on structural stress and deformation, CFD emphasizes fluid behavior, flow patterns, pressure distribution, and velocity fields to predict fluid-structure interactions and optimize designs in aerospace, automotive, and chemical engineering.
Key Differences Between FEA and CFD
Finite Element Analysis (FEA) primarily focuses on structural mechanics, analyzing stress, strain, and deformation in solid materials under various loads, while Computational Fluid Dynamics (CFD) deals with fluid flow behavior, heat transfer, and turbulence within liquids and gases. FEA models are typically discretized into finite elements such as tetrahedrons or hexahedrons to solve equations related to solid mechanics, whereas CFD employs mesh grids or control volumes to solve Navier-Stokes equations governing fluid motion. The key distinction lies in FEA's application to static or dynamic structural problems, contrasted with CFD's capability to simulate fluid dynamics phenomena including laminar or turbulent flow.
Applications of FEA in Mechanical Engineering
Finite Element Analysis (FEA) is extensively applied in mechanical engineering for stress analysis, thermal management, and structural optimization of components such as automotive parts, aerospace structures, and manufacturing equipment. FEA enables engineers to simulate deformation, fatigue, and failure modes under various load conditions, enhancing product durability and performance. Unlike Computational Fluid Dynamics (CFD), which focuses on fluid flow and heat transfer, FEA primarily addresses solid mechanics challenges in complex mechanical systems.
Applications of CFD in Mechanical Engineering
Computational Fluid Dynamics (CFD) plays a crucial role in mechanical engineering by enabling the simulation of fluid flow, heat transfer, and related phenomena within systems such as HVAC, automotive aerodynamics, and turbine design. Unlike Finite Element Analysis (FEA), which primarily focuses on structural simulations, CFD optimizes the design and performance of components subjected to fluid interactions by solving Navier-Stokes equations numerically. Applications include the study of airflow patterns, thermal management, and multiphase flows essential for improving efficiency and safety in mechanical systems.
Advantages and Limitations of FEA
Finite Element Analysis (FEA) excels in structural analysis by accurately predicting stress, strain, and deformation in complex geometries under various loading conditions, making it indispensable for designing mechanical components and evaluating material performance. Its limitations include less suitability for simulating fluid flow phenomena and challenges in modeling highly nonlinear dynamic behavior or multiphysics interactions without advanced coupling techniques. FEA requires fine meshing for precise results, which can lead to high computational costs and longer processing times in large-scale models.
Advantages and Limitations of CFD
Computational Fluid Dynamics (CFD) excels in simulating fluid flow, heat transfer, and related phenomena with high spatial and temporal resolution, enabling detailed analysis of complex fluid behaviors that Finite Element Analysis (FEA) might not capture accurately. CFD's advantages include precise visualization of turbulence, pressure distribution, and velocity fields, which are crucial in aerospace, automotive, and environmental engineering. Limitations of CFD involve high computational cost, sensitivity to mesh quality, and challenges in modeling multiphase flows or chemically reacting systems, requiring extensive validation to ensure reliable predictions.
Software Tools for FEA and CFD
ANSYS, Abaqus, and COMSOL Multiphysics dominate as leading software tools for Finite Element Analysis (FEA), offering robust solvers for structural, thermal, and electromagnetic simulations. For Computational Fluid Dynamics (CFD), software like STAR-CCM+, OpenFOAM, and Fluent provide advanced capabilities in fluid flow, heat transfer, and turbulence modeling. These platforms support multiphysics coupling, enabling integrated analysis of fluid-structure interactions and enhancing design optimization across engineering disciplines.
Choosing Between FEA and CFD for Mechanical Design
Finite Element Analysis (FEA) excels in assessing structural integrity, stress distribution, and deformation of mechanical components, making it ideal for solid mechanics problems. Computational Fluid Dynamics (CFD) specializes in simulating fluid flow, heat transfer, and aerodynamic behavior, crucial for fluid-structure interaction and thermal analysis. Selecting between FEA and CFD depends on the nature of the mechanical design challenge, prioritizing structural performance for FEA and fluid dynamics optimization for CFD applications.
Mesh generation
Finite element analysis (FEA) utilizes mesh generation primarily for structural discretization with elements like tetrahedrons or hexahedrons, while computational fluid dynamics (CFD) requires mesh generation optimized for fluid flow accuracy, often using finer, anisotropic meshes adaptable to complex geometries and boundary layers.
Boundary conditions
Finite element analysis requires precise mechanical boundary conditions to model structural constraints, while computational fluid dynamics relies on fluid flow boundary conditions such as velocity, pressure, and turbulence parameters to simulate fluid behavior accurately.
Discretization methods
Finite element analysis uses mesh-based discretization with elements like triangles or tetrahedra to solve solid mechanics problems, while computational fluid dynamics employs grid-based discretization, such as structured or unstructured grids, to model fluid flow behavior.
Stress-strain response (FEA)
Finite element analysis precisely predicts stress-strain responses by discretizing solids into elements, while computational fluid dynamics primarily models fluid flow and does not directly analyze material deformation under stress.
Navier-Stokes equations (CFD)
Computational Fluid Dynamics (CFD) uses Navier-Stokes equations to model fluid flow and turbulence, while Finite Element Analysis (FEA) primarily focuses on structural mechanics and solid deformation simulations.
Element interpolation functions
Finite element analysis uses polynomial element interpolation functions to approximate solutions within elements, while computational fluid dynamics employs specialized interpolation schemes to accurately capture fluid flow properties and turbulence.
Turbulence modeling (CFD)
Turbulence modeling in computational fluid dynamics accurately predicts fluid flow behavior and energy dissipation, while finite element analysis primarily focuses on structural stress and deformation without inherently addressing fluid turbulence.
Structural deformation (FEA)
Finite element analysis (FEA) precisely predicts structural deformation by subdividing complex geometries into smaller elements to simulate stress, strain, and displacement under applied loads.
Solver algorithms
Finite element analysis solver algorithms primarily use iterative methods for structural deformation simulations, whereas computational fluid dynamics solvers employ discretization techniques like finite volume and advanced turbulence models to accurately simulate fluid flow.
Convergence criteria
Finite Element Analysis achieves convergence by minimizing residual errors in structural equations through iterative mesh refinement, while Computational Fluid Dynamics relies on convergence criteria involving mass, momentum, and energy conservation errors to ensure solution stability and accuracy.
Finite element analysis vs computational fluid dynamics Infographic
 njnir.com
njnir.com