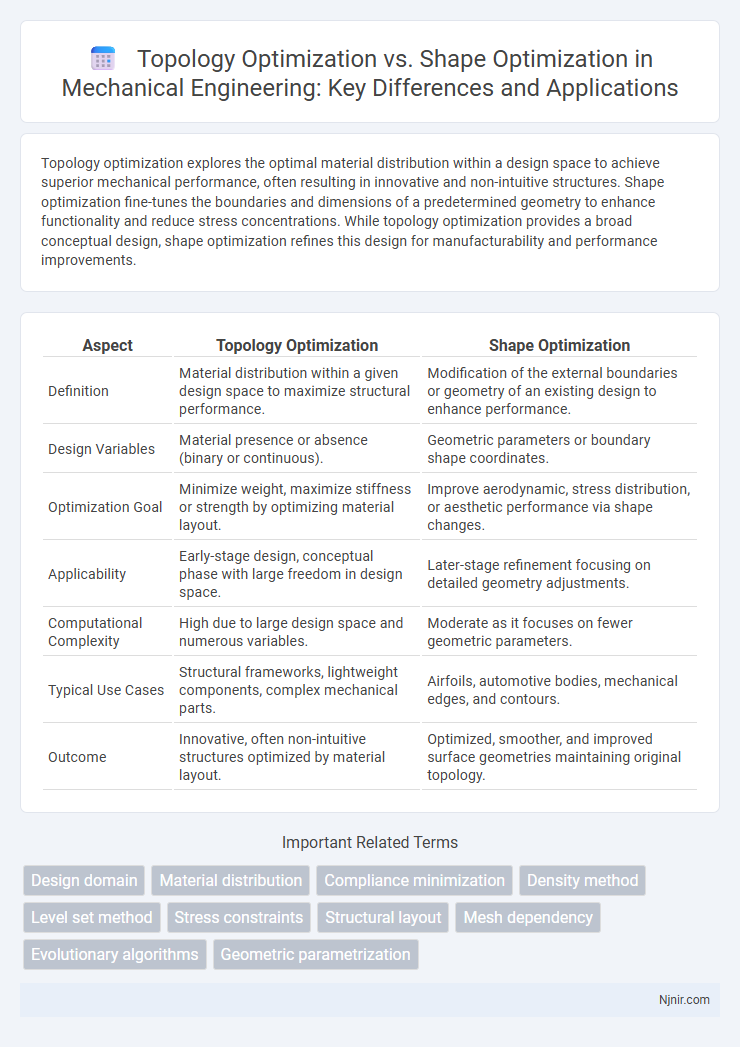
Topology optimization explores the optimal material distribution within a design space to achieve superior mechanical performance, often resulting in innovative and non-intuitive structures. Shape optimization fine-tunes the boundaries and dimensions of a predetermined geometry to enhance functionality and reduce stress concentrations. While topology optimization provides a broad conceptual design, shape optimization refines this design for manufacturability and performance improvements.
Table of Comparison
| Aspect | Topology Optimization | Shape Optimization |
|---|---|---|
| Definition | Material distribution within a given design space to maximize structural performance. | Modification of the external boundaries or geometry of an existing design to enhance performance. |
| Design Variables | Material presence or absence (binary or continuous). | Geometric parameters or boundary shape coordinates. |
| Optimization Goal | Minimize weight, maximize stiffness or strength by optimizing material layout. | Improve aerodynamic, stress distribution, or aesthetic performance via shape changes. |
| Applicability | Early-stage design, conceptual phase with large freedom in design space. | Later-stage refinement focusing on detailed geometry adjustments. |
| Computational Complexity | High due to large design space and numerous variables. | Moderate as it focuses on fewer geometric parameters. |
| Typical Use Cases | Structural frameworks, lightweight components, complex mechanical parts. | Airfoils, automotive bodies, mechanical edges, and contours. |
| Outcome | Innovative, often non-intuitive structures optimized by material layout. | Optimized, smoother, and improved surface geometries maintaining original topology. |
Introduction to Topology and Shape Optimization
Topology optimization focuses on determining the optimal material distribution within a given design space to maximize structural performance, often leading to innovative and non-intuitive geometries. Shape optimization fine-tunes the boundaries and contours of a predefined structure to improve performance criteria such as stress distribution, aerodynamic efficiency, or weight reduction. Both methods serve crucial roles in engineering design, with topology optimization providing a broader design freedom while shape optimization refines existing configurations.
Fundamental Principles of Topology Optimization
Topology optimization focuses on determining the optimal material distribution within a given design space for maximum structural performance, based on fundamental principles such as minimum compliance and stress constraints. Shape optimization, in contrast, refines the boundaries of an existing geometry without altering the material layout. The core principle of topology optimization involves iterative material redistribution governed by finite element analysis and sensitivity analysis to achieve an optimal stiffness-to-weight ratio.
Core Concepts of Shape Optimization
Shape optimization focuses on refining the geometry of a structure by modifying its boundary to improve performance metrics such as stress distribution, weight reduction, or aerodynamic efficiency. It uses gradient-based methods to iteratively adjust the shape while maintaining the original topology, ensuring manufacturability and design constraints are met. Unlike topology optimization, which creates material distribution from scratch, shape optimization optimizes within an existing design framework for enhanced structural integrity and functionality.
Mathematical Formulation and Algorithms
Topology optimization mathematically formulates design problems by distributing material within a given domain to minimize an objective function, typically expressed through density variables governed by partial differential equations and often solved using gradient-based algorithms such as the Solid Isotropic Material with Penalization (SIMP) method. Shape optimization focuses on modifying the boundary geometry to optimize performance criteria, employing shape derivatives and boundary parameterizations, solved via algorithms like boundary element methods or adjoint-based gradient descent. Both approaches rely on sensitivity analysis but differ fundamentally in variable representation and computational strategies, with topology optimization handling discrete material distribution and shape optimization adjusting continuous boundary contours.
Design Variables and Constraints
Topology optimization uses a high number of design variables representing material distribution within a design domain, allowing for complex, non-intuitive geometries. Shape optimization involves fewer design variables that define explicit geometric parameters such as curves, edges, or surfaces, focusing on fine-tuning existing shapes. Constraints in topology optimization often include volume fraction and manufacturability, while shape optimization constraints typically address boundary conditions, smoothness, and feature size for practical fabrication.
Performance Comparison: Efficiency and Results
Topology optimization generally achieves higher structural efficiency by exploring a broader design space and identifying innovative load paths, often yielding superior stiffness-to-weight ratios compared to shape optimization. Shape optimization, while more computationally efficient due to fewer design variables and constraints, primarily refines existing geometries, resulting in improved but less radical performance gains. Empirical studies demonstrate topology optimization excels in maximizing performance metrics such as stiffness and strength, whereas shape optimization provides faster convergence and easier manufacturability adjustments.
Applications in Mechanical Engineering
Topology optimization maximizes structural performance by distributing material within a given design space, critical for lightweight component design in aerospace and automotive engineering. Shape optimization refines existing geometries for stress concentration reduction and aerodynamic improvements in mechanical parts such as turbine blades and automotive body panels. Combining both methods enhances efficiency and durability in complex mechanical systems, including robotic arms and load-bearing structures.
Software Tools and Implementation
Topology optimization software like Abaqus, ANSYS, and Altair OptiStruct enable material distribution analysis within a design space, facilitating innovative lightweight structures, while shape optimization tools such as Siemens NX and SolidWorks focus on refining boundary geometries for performance enhancement. Implementation in topology optimization involves iterative finite element analysis (FEA) paired with gradient-based algorithms to remove inefficient material, contrasting with shape optimization which modifies surface parameters guided by sensitivity analysis and CAD integration. Choosing between these approaches depends on project goals, where topology optimization suits conceptual design phases and shape optimization excels in detailed design refinement with seamless CAD interoperability.
Limitations and Challenges
Topology optimization often faces challenges related to high computational cost and mesh dependency, limiting its applicability in large-scale or real-time problems. Shape optimization, while less computationally intensive, struggles with local minima and requires a predefined topology, restricting design freedom. Both methods encounter difficulties in accurately incorporating manufacturing constraints and material nonlinearities, impacting the feasibility of optimized designs.
Future Trends in Structural Optimization
Future trends in structural optimization emphasize integrating topology optimization and shape optimization to leverage their complementary strengths in material distribution and geometric refinement. Advances in computational power and machine learning algorithms enable real-time, multi-scale optimization, resulting in innovative, lightweight, and high-performance structures for aerospace, automotive, and civil engineering applications. The development of additive manufacturing further accelerates the practical implementation of complex, optimized designs previously unachievable through traditional fabrication methods.
Design domain
Topology optimization explores the entire design domain to determine optimal material distribution, while shape optimization modifies the boundaries within a fixed design domain to improve performance.
Material distribution
Topology optimization strategically distributes material by removing inefficient regions, whereas shape optimization fine-tunes the boundaries of a predefined structure without altering the overall material layout.
Compliance minimization
Topology optimization typically delivers superior compliance minimization compared to shape optimization by allowing material distribution changes within a design domain rather than just refining boundaries.
Density method
Density method in topology optimization uses material distribution within a design domain to maximize structural performance, while shape optimization adjusts boundary interfaces without altering the internal topology.
Level set method
The Level Set method in topology optimization offers superior handling of complex boundary evolutions and shape changes compared to traditional shape optimization techniques, enabling more flexible material distribution and optimized structural performance.
Stress constraints
Topology optimization efficiently distributes material to minimize stress concentrations under complex stress constraints, while shape optimization refines boundaries to enhance stress distribution within predefined topologies.
Structural layout
Topology optimization maximizes structural layout efficiency by determining optimal material distribution within a design space, while shape optimization refines the boundaries of a fixed topology to improve performance.
Mesh dependency
Topology optimization often exhibits higher mesh dependency due to its element-wise material distribution approach, whereas shape optimization typically involves boundary parametrization that results in lower sensitivity to mesh discretization.
Evolutionary algorithms
Evolutionary algorithms excel in topology optimization by efficiently exploring complex design spaces to identify optimal material distributions, whereas shape optimization focuses on refining boundary geometries for performance improvements.
Geometric parametrization
Topology optimization uses pixel or voxel-based geometric parametrization for material distribution, whereas shape optimization relies on boundary-based geometric parametrization to refine existing design contours.
Topology optimization vs shape optimization Infographic
 njnir.com
njnir.com